Problem 12.10

Fundamentals of Solar Cells and Photovoltaic Systems Engineering

Solutions Manual - Chapter 12

Problem 12.10

Given the QE of a silicon test cell and a calibrated cell, obtain their respective SR and calculate the Spectral Mismatch Factor \(M_f\), when the test cell is measured using a Xe-arc lamp, relative to the reference spectrum AM1.5G.

We will use the package pandas to handle the data and matplotlib.pyplot to plot the results.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

We start by importing the data for the solar spectra.

reference = pd.read_csv('data/Reference_spectrum_ASTM-G173-03.csv', index_col=0, header=0) 
reference

	AM0	AM1.5G	AM1.5D
Wvlgth nm	Etr W*m-2*nm-1	Global tilt W*m-2*nm-1	Direct+circumsolar W*m-2*nm-1
280	8.20E-02	4.73E-23	2.54E-26
280.5	9.90E-02	1.23E-21	1.09E-24
281	1.50E-01	5.69E-21	6.13E-24
281.5	2.12E-01	1.57E-19	2.75E-22
...	...	...	...
3980	8.84E-03	7.39E-03	7.40E-03
3985	8.80E-03	7.43E-03	7.45E-03
3990	8.78E-03	7.37E-03	7.39E-03
3995	8.70E-03	7.21E-03	7.23E-03
4000	8.68E-03	7.10E-03	7.12E-03

2003 rows × 3 columns

reference.drop(reference.index[0], inplace=True)   # remove row including information on units
reference=reference.astype(float)                  # convert values to float for easy operation
reference.index=reference.index.astype(float)      # convert indexes to float for easy operation

We import the data for the Xe-arc lamp.

xe_arc = pd.read_csv('data/Xe lamp spectral irradiance.csv', index_col=0, header=0) 
xe_arc

	Xe arc lamp (W*m-2*nm-1)
wavelength (nm)
300.36966	0.000793
300.58005	0.000816
300.79044	0.000837
301.00082	0.000858
301.21124	0.000876
...	...
1199.77246	0.213920
1199.84302	0.213600
1199.91345	0.213280
1199.98401	0.212960
1200.05444	0.212640

6283 rows × 1 columns

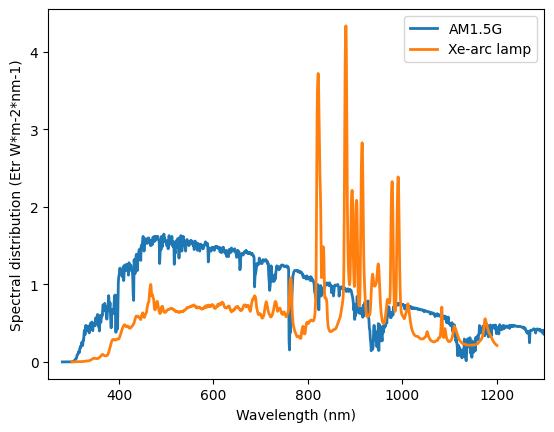
We can also plot the AM1.5G spectra and the Xe-arc lamp spectra.

plt.plot(reference['AM1.5G'], 
         linewidth=2, label='AM1.5G')
plt.plot(xe_arc, 
         linewidth=2, label='Xe-arc lamp')
plt.ylabel('Spectral distribution (Etr W*m-2*nm-1)')
plt.xlabel('Wavelength (nm)')
plt.xlim([250,1300])
plt.legend()

<matplotlib.legend.Legend at 0x7f24c0598e90>

We define the relevant constants and retrieve the QE of the silicon solar cell (device under test), and the callibrated cell.

h=6.63*10**(-34)   # [J·s] Planck constant
e=1.60*10**(-19)   # [C] electron charge
c =299792458       #[m/s] Light speed

QE_dut = pd.read_csv('data/QE_DUT.csv', index_col=0, header=0) 
QE_cal= pd.read_csv('data/QE_calibrated_cell.csv', index_col=0, header=0) 

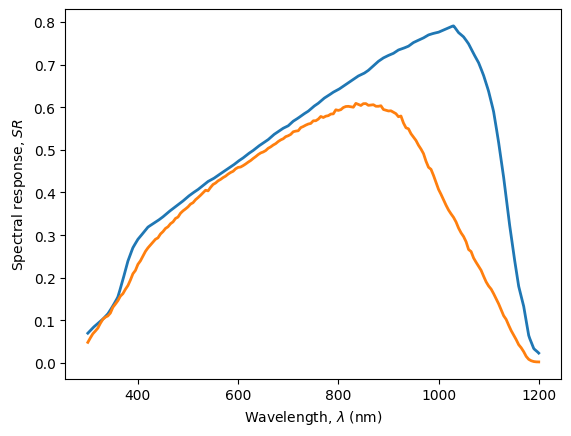
We calculate the Spectral Response (SR) of both cells and plot them.

SR_dut=pd.Series(index=QE_dut.index,
            data=[QE_dut.loc[i,'QE']*e*i*0.000000001/(h*c) for i in QE_dut.index])
SR_cal=pd.Series(index=QE_cal.index,
            data=[QE_cal.loc[i,'QE']*e*i*0.000000001/(h*c) for i in QE_cal.index])
plt.plot(SR_dut, 
         linewidth=2)
plt.plot(SR_cal, 
         linewidth=2)
plt.ylabel('Spectral response, $SR$')
plt.xlabel(r'Wavelength, $\lambda$ (nm)');

For every spectra and solar cell, we interpolate the spectrum at those datapoints included in the SR, and integrate to obtain the short-circuit current density using Eq. 3.5.

\(J_{L, spectrum, cell}=\int SR(\lambda) \cdot G(\lambda) \ d\lambda\)

spectra=xe_arc['Xe arc lamp (W*m-2*nm-1)']
spectra_interpolated=np.interp(SR_dut.index, spectra.index, spectra.values)
J_sim_dut = np.trapz([x*y for x,y in zip(SR_dut, spectra_interpolated)], x=SR_dut.index)*1000/10000 # A-> mA ; m2 -> cm2
spectra_interpolated=np.interp(SR_cal.index, spectra.index, spectra.values)
J_sim_cal = np.trapz([x*y for x,y in zip(SR_cal, spectra_interpolated)], x=SR_cal.index)*1000/10000 # A-> mA ; m2 -> cm2

spectra=reference['AM1.5G']
spectra_interpolated=np.interp(SR_dut.index, spectra.index, spectra.values)
J_ref_dut =np.trapz([x*y for x,y in zip(SR_dut, spectra_interpolated)], x=SR_dut.index)*1000/10000 # A-> mA ; m2 -> cm2

spectra_interpolated=np.interp(SR_cal.index, spectra.index, spectra.values)
J_ref_cal =np.trapz([x*y for x,y in zip(SR_cal, spectra_interpolated)], x=SR_cal.index)*1000/10000 # A-> mA ; m2 -> cm2

We calculate the Spectral Mismatch Factor \(M_f\) using Eq. 12.3

\(M_f=\frac{J_{L, sim, dut}}{J_{L, ref, dut}}\frac{J_{L, ref, cal}}{J_{L, sim, cal}}\)

M_f=J_sim_dut/J_ref_dut*J_ref_cal/J_sim_cal
print('Spectral Mismatch Factor = ' + str(M_f.round(3)))

Spectral Mismatch Factor = 1.043