Problem 5.8

Fundamentals of Solar Cells and Photovoltaic Systems Engineering

Solutions Manual - Chapter 5

Problem 5.8

Design an antireflective coating (ARC), finding its refractive index and thickness, to minimize the light power lost by reflection in a silicon solar cell with a pyramid-shaped texturing, under the AM1.5 G solar spectrum. For this, consider that the refractive index of the ARC material is constant with wavelength, and plot the reflected power in the wavelength range 300-1100 nm against the refractive index and the thickness of the ARC. What is the optimum refractive index and thickness of the ARC layer?

First, we import the Python modules used and define the number of datapoints to use in the calculated data

import math
import numpy as np
import matplotlib.pyplot as plt

DATA_SIZE = 50

We load the data for silicon refractive index and AM1.5G solar spectrum

# Load nk and solar spectrum data
# We assume the data is in the same folder as the notebook file

#Data columns: wavelength(nm) refractive_index extinction_coefficient
Si_nk = np.loadtxt("data/Si_nk.txt", skiprows=2, delimiter='\t')

#Data columns: wavelength(nm) spectral_irradiance (W·m-2·nm-1)
AM15G = np.loadtxt("data/am15g_G173_W.txt", skiprows=1, delimiter='\t')

Calculate the spectral reflectivity at normal incidence

# Create data waves
# First estimate the data ranges
# Refractive index: the optimum must be around the middle between Si and air: from 1.5 to 2.5
min_n = 1.5
max_n = 2.5
n_ARC = np.zeros((DATA_SIZE,2))
n_ARC = np.linspace(min_n, max_n, DATA_SIZE)

# Thickness: maximum could be 1100/(4*1.5) = 183 nm
# Mínimum: 300/(4*2.5) = 30
min_thick = 30
max_thick = 183
thick_ARC = np.zeros((DATA_SIZE,2))
thick_ARC = np.linspace(min_thick, max_thick, DATA_SIZE)

# Final data: reflected power
rfl_power = np.zeros((DATA_SIZE,DATA_SIZE))

# Reflectivity data
# We downsample the n data to speed up calculations
min_wv = 300    #Minimum wavelength
max_wv = 1100   #Maximum wavelength
step_wv = 10
nData = int((max_wv-min_wv)/step_wv)

# Spectral reflected power
Rflw = np.zeros((nData,2))
Rflw[:,0] = np.linspace(min_wv, max_wv, nData)

Calculate the reflected power for the range of n and thicknesses set

# Sweep n
for x in range(DATA_SIZE):
    # Sweep thickness
    for y in range(DATA_SIZE):
        # Sweep wavelength
        
        for z in range(nData):
            nSi = np.interp(Rflw[z,0], Si_nk[:,0],Si_nk[:,1])
            r01 = (1-n_ARC[x])/(1+n_ARC[x])
            r12 = (n_ARC[x]-nSi)/(n_ARC[x]+nSi)
            theta = 2*math.pi*n_ARC[x]*thick_ARC[y]/Rflw[z,0]
            Rflw[z,1] = (r01**2 + r12**2 + 2*r01*r12*math.cos(2*theta))/(1+ r01**2 * r12**2 + 2*r01*r12*math.cos(2*theta))
 
            Rflw[z,1] *= np.interp(Rflw[z,0], AM15G[:,0],AM15G[:,1])
            
        rfl_power[x,y] = np.trapz(Rflw[:,1], x=Rflw[:,0], axis=0)
        

Plot the data

fig, ax = plt.subplots()
CS = ax.contour(n_ARC, thick_ARC, rfl_power, 20)
plt.xlabel('ARC refractive index', size=14)
plt.ylabel('ARC thickness (nm)', size=14)

ax.clabel(CS, CS.levels, inline=True, fontsize=10)
ax.set_title("Reflected power density (W·m$^{-2}$)")

# Save figure
plt.savefig("fig_S5.8.png", dpi=300)

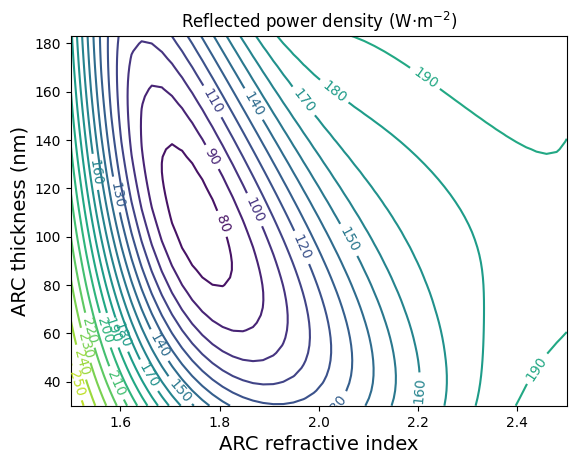
We obtain a maximum power for a refractive index around 1.8 and thickness around 110 nm. In practice, this refractive index may not be possible to attain with the materials available. For SiNx, with a higher refractive index, the optimum thickness is lower, around 70-80 nm.