Problem 2.1

Fundamentals of Solar Cells and Photovoltaic Systems Engineering

Solutions Manual - Chapter 2

Problem 2.1

The temperature of the surface of the Sun is 5780 K.

(a) Assuming that the Sun is a black body, calculate the total radiant emittance in W/m\(^2\) and the wavelength at which emission peaks.

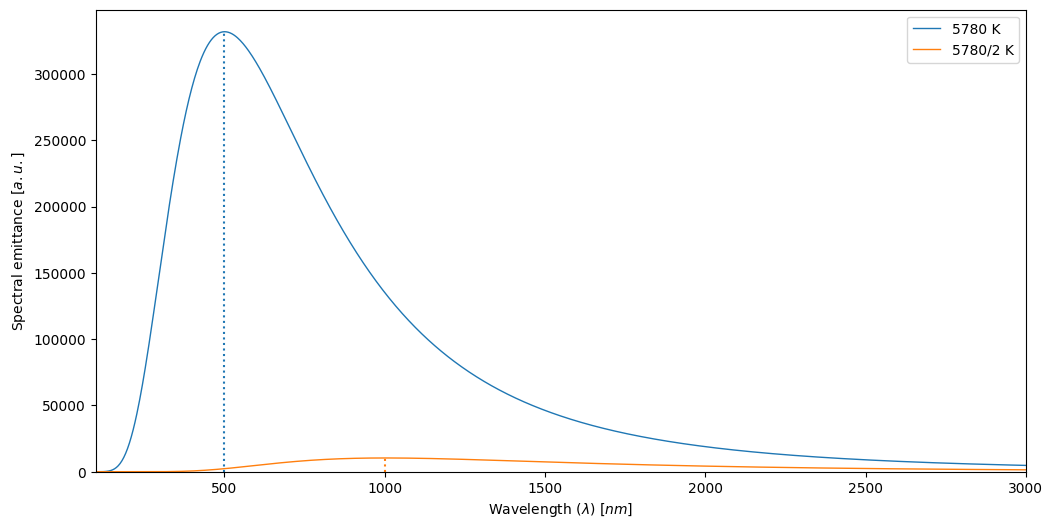
(b) Consider a hypothetical future in which the Sun temperature has decreased to half that of today.

Calculate how the radiant emittance and peak would change for both temperatures and draw a freehand sketch of the spectral distribution of the Sun’s emittance of both temperatures with arbitrary units. Discuss the differences.

We will use the package matplotlib.pyplot to plot the results.

import matplotlib.pyplot as plt
import numpy as np
from scipy import constants

We start by defining the Planck’s law

WV_INI = 100 # [nm]
WV_MAX = 3000 # [nm]

h = constants.h # 6.626e-34 [J·s]
c = constants.speed_of_light # 3.0e+8 [m/s]
k_B = constants.Boltzmann # 1.38e-23 [J/K]
π = constants.pi # 3.141592
planck_law = lambda λ, T: 8 * π * h * c ** 2 / (λ**5) * 1 / (np.exp(h * c / (λ * k_B * T)) - 1) * 1e-9

And then we plot spectral emittances

fig, ax = plt.subplots(figsize=(12, 6))

wavelengths = np.linspace(start=WV_INI, stop=WV_MAX, num=1000) # [nm]

solid_angle_arbitrary = 1

emittance_5780 = planck_law(λ=wavelengths*1e-9, T=5780)
emittance_5780_2 = planck_law(λ=wavelengths*1e-9, T=5780/2)

ax.plot(wavelengths, emittance_5780, linewidth=1, label='5780 K')
ax.plot(wavelengths, emittance_5780_2, linewidth=1, label='5780/2 K')

ax.vlines(x=wavelengths[emittance_5780.argmax()], ymin=0, ymax=emittance_5780.max(), linestyle=':', color='C0')
ax.vlines(x=wavelengths[emittance_5780_2.argmax()], ymin=0, ymax=emittance_5780_2.max(), linestyle=':', color='C1')

ax.legend()

ax.set_ylim(bottom=0)
ax.set_xlim([WV_INI, WV_MAX])

ax.set_xlabel("Wavelength ($\lambda$) [$nm$]")
ax.set_ylabel("Spectral emittance [$a.u.$]")

Text(0, 0.5, 'Spectral emittance [$a.u.$]')