Problem 5.2

Fundamentals of Solar Cells and Photovoltaic Systems Engineering

Solutions Manual - Chapter 5

Problem 5.2

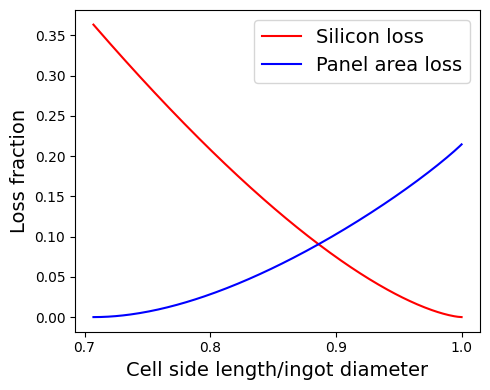
Silicon solar cells are going to be manufactured from a Czochralski-grown silicon ingot. To decide if the solar cells should have a full-square (FSQ) or pseudo-square (PSQ) geometry, the losses incurred in each case must be calculated. To that end, plot, as a function of the solar cell side length, the percentage of silicon material lost and the percentage of panel surface lost. You can assume that the distance between cells in the panel is negligible.

import math
import numpy as np
import matplotlib.pyplot as plt

DATA_SIZE = 200

# Previous data
ingot_D = 30  # Ingot diameter (cm). The results do not depend on this number, though!
# The maximum cell side length is the diameter of the ingot (round solar cell)
max_cell_sideL = ingot_D
# The smallest cell is inscribed in the original ingot, hence:
min_cell_sideL = ingot_D/math.sqrt(2)

# Silicon material volume lost
# Note that it is the same as area loss, since the ingot length is constant
Si_area_lost = np.zeros((DATA_SIZE,2))
# We compute the loss for a the range of possible cell side lengths
Si_area_lost[:,0] = np.linspace(min_cell_sideL, max_cell_sideL, DATA_SIZE)
# You can look up how the area of a circle sector is calculated. We calculate here 4 times that area
Si_area_lost[:,1] = (2/math.pi)*((2*np.arccos(Si_area_lost[:,0]/ingot_D)-np.sin(2*np.arccos(Si_area_lost[:,0]/ingot_D))))   

# Cell area lost in the final PV panel
Cell_area_lost = np.zeros((DATA_SIZE,2))
Cell_area_lost[:,0] = np.linspace(min_cell_sideL, max_cell_sideL, DATA_SIZE)
# We calculate it in steps.
# We need to calculate the area of the cropped corners in the cell
# Note this is the area of the cell square minus the area of the ingot circle cropped by the cell square 
# 1. Area of the cell square
Cell_area_lost[:,1] = Cell_area_lost[:,0]**2
# 2. Area of the full ingot section minus the cropped areas (calculated above)
Cell_area_lost[:,1] -= math.pi*(ingot_D/2)**2 
Cell_area_lost[:,1] += (0.5*ingot_D**2)*(2*np.arccos(Si_area_lost[:,0]/ingot_D)-np.sin(2*np.arccos(Si_area_lost[:,0]/ingot_D)))
# 3. Divide by the cell square area to obtain the fraction lost
Cell_area_lost[:,1] /= Cell_area_lost[:,0]**2   

Si_area_lost[:,0]/=ingot_D
Cell_area_lost[:,0]/=ingot_D

fig = plt.figure(figsize=[5,4], tight_layout=True)
ax = fig.add_subplot()    
ax.set_xlabel('Cell side length/ingot diameter', size=14)
ax.set_ylabel('Loss fraction', size=14)
plt.rc('xtick', labelsize=14) 
plt.rc('ytick', labelsize=14)

trace, = ax.plot(Si_area_lost[:,0], Si_area_lost[:,1], 'r-', label='Silicon loss' )
trace, = ax.plot(Cell_area_lost[:,0], Cell_area_lost[:,1], 'b-', label='Panel area loss' )

ax.legend(fontsize=14);

# Save figure
plt.savefig("fig_S5.X.png", dpi=300)

# Print results
print("Note the large losses involved:")
print("· Maximum silicon material loss fraction: " + str(f"{np.max(Si_area_lost[:,1]):.3}"))
print("· Maximum panel area loss fraction: " + str(f"{np.max(Cell_area_lost[:,1]):.3}"))

Note the large losses involved:
· Maximum silicon material loss fraction: 0.363
· Maximum panel area loss fraction: 0.215