Problem 8.2#
Integrated Energy Grids
Problem 8.2. Join capacity and dispatch optimization with storage.
Use the model described in Problem 8.1 and add the possibility of installing battery storage. The annualized capital cost of the battery comprises 12,894 EUR/MWh/a for the energy capacity and 24,678 EUR/MW/a for the inverter. The inverter efficiency is 0.96 and the battery is assumed to have a fixed energy-to-power ratio of 2 hours. Assume also an existing Combined Cycled Gas Turbine (CCGT) unit with an electricity generation capacity of 6 GW. The annualized capital cost and marginal generation costs for the CCGT are respectively 104,788 EUR/MW/a and 46.8 EUR/MWh.
a) Calculate the optimal installed capacities and plot the hourly generation and demand during January.
b) How does the CCGT power plant recover its cost?
c) How does the battery recover its cost?
Note
If you have not yet set up Python on your computer, you can execute this tutorial in your browser via Google Colab. Click on the rocket in the top right corner and launch “Colab”. If that doesn’t work download the .ipynb file and import it in Google Colab.
Then install pandas and numpy by executing the following command in a Jupyter cell at the top of the notebook.
!pip install pandas pypsa
Note
See also https://model.energy.
In this exercise, we want to build a replica of model.energy. This tool calculates the cost of meeting a constant electricity demand from a combination of wind power, solar power and storage for different regions of the world. We deviate from model.energy by including electricity demand profiles rather than a constant electricity demand.
import matplotlib.pyplot as plt
import pandas as pd
import pypsa
Prerequisites: handling technology data and costs#
We maintain a database (PyPSA/technology-data) which collects assumptions and projections for energy system technologies (such as costs, efficiencies, lifetimes, etc.) for given years, which we can load into a pandas.DataFrame. This requires some pre-processing to load (e.g. converting units, setting defaults, re-arranging dimensions):
year = 2030
url = f"https://raw.githubusercontent.com/PyPSA/technology-data/master/outputs/costs_{year}.csv"
costs = pd.read_csv(url, index_col=[0, 1])
costs.loc[costs.unit.str.contains("/kW"), "value"] *= 1e3
costs.unit = costs.unit.str.replace("/kW", "/MW")
defaults = {
"FOM": 0,
"VOM": 0,
"efficiency": 1,
"fuel": 0,
"investment": 0,
"lifetime": 25,
"CO2 intensity": 0,
"discount rate": 0.07,
}
costs = costs.value.unstack().fillna(defaults)
costs.at["OCGT", "fuel"] = costs.at["gas", "fuel"]
costs.at["CCGT", "fuel"] = costs.at["gas", "fuel"]
costs.at["OCGT", "CO2 intensity"] = costs.at["gas", "CO2 intensity"]
costs.at["CCGT", "CO2 intensity"] = costs.at["gas", "CO2 intensity"]
Let’s also write a small utility function that calculates the annuity to annualise investment costs. The formula is
where \(r\) is the discount rate and \(n\) is the lifetime.
def annuity(r, n):
return r / (1.0 - 1.0 / (1.0 + r) ** n)
annuity(0.07, 20)
0.09439292574325567
Based on this, we can calculate the marginal generation costs (€/MWh):
costs["marginal_cost"] = costs["VOM"] + costs["fuel"] / costs["efficiency"]
and the annualised investment costs (capital_cost in PyPSA terms, €/MW/a):
annuity = costs.apply(lambda x: annuity(x["discount rate"], x["lifetime"]), axis=1)
costs["capital_cost"] = (annuity + costs["FOM"] / 100) * costs["investment"]
We can now read the capital and marginal cost of onshore wind, solar and OCGT
costs.at["onwind", "capital_cost"] #EUR/MW/a
np.float64(101644.12332388277)
costs.at["solar", "capital_cost"] #EUR/MW/a
np.float64(51346.82981964593)
costs.at["OCGT", "capital_cost"] #EUR/MW/a
np.float64(47718.67056370105)
costs.at["OCGT", "marginal_cost"] #EUR/MWh
np.float64(64.6839512195122)
costs.at["CCGT", "capital_cost"] #EUR/MW/a
np.float64(104788.02078332388)
costs.at["CCGT", "marginal_cost"] #EUR/MWh
np.float64(46.803120689655174)
costs.at["battery inverter", "capital_cost"]
np.float64(24798.913824044732)
costs.at["battery storage", "capital_cost"]
np.float64(12957.628369768725)
costs.at["battery inverter", "efficiency"]
np.float64(0.96)
Retrieving time series data#
In this example, wind data from https://zenodo.org/record/3253876#.XSiVOEdS8l0 and solar PV data from https://zenodo.org/record/2613651#.X0kbhDVS-uV is used. The data is downloaded in csv format and saved in the ‘data’ folder. The Pandas package is used as a convenient way of managing the datasets.
For convenience, the column including date information is converted into Datetime and set as index
data_solar = pd.read_csv('data/pv_optimal.csv',sep=';')
data_solar.index = pd.DatetimeIndex(data_solar['utc_time'])
data_wind = pd.read_csv('data/onshore_wind_1979-2017.csv',sep=';')
data_wind.index = pd.DatetimeIndex(data_wind['utc_time'])
data_el = pd.read_csv('data/electricity_demand.csv',sep=';')
data_el.index = pd.DatetimeIndex(data_el['utc_time'])
The data format can now be analyzed using the .head() function to show the first lines of the data set
data_solar.head()
| utc_time | AUT | BEL | BGR | BIH | CHE | CYP | CZE | DEU | DNK | ... | MLT | NLD | NOR | POL | PRT | ROU | SRB | SVK | SVN | SWE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| utc_time | |||||||||||||||||||||
| 1979-01-01 00:00:00+00:00 | 1979-01-01T00:00:00Z | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1979-01-01 01:00:00+00:00 | 1979-01-01T01:00:00Z | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1979-01-01 02:00:00+00:00 | 1979-01-01T02:00:00Z | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1979-01-01 03:00:00+00:00 | 1979-01-01T03:00:00Z | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1979-01-01 04:00:00+00:00 | 1979-01-01T04:00:00Z | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
5 rows × 33 columns
We will use timeseries for Portugal in this excercise
country = 'PRT'
Join capacity and dispatch optimization#
For building the model, we start again by initialising an empty network, adding the snapshots, and the electricity bus.
n = pypsa.Network()
hours_in_2015 = pd.date_range('2015-01-01 00:00Z',
'2015-12-31 23:00Z',
freq='h')
n.set_snapshots(hours_in_2015.values)
n.add("Bus",
"electricity")
n.snapshots
DatetimeIndex(['2015-01-01 00:00:00', '2015-01-01 01:00:00',
'2015-01-01 02:00:00', '2015-01-01 03:00:00',
'2015-01-01 04:00:00', '2015-01-01 05:00:00',
'2015-01-01 06:00:00', '2015-01-01 07:00:00',
'2015-01-01 08:00:00', '2015-01-01 09:00:00',
...
'2015-12-31 14:00:00', '2015-12-31 15:00:00',
'2015-12-31 16:00:00', '2015-12-31 17:00:00',
'2015-12-31 18:00:00', '2015-12-31 19:00:00',
'2015-12-31 20:00:00', '2015-12-31 21:00:00',
'2015-12-31 22:00:00', '2015-12-31 23:00:00'],
dtype='datetime64[ns]', name='snapshot', length=8760, freq=None)
We add all the technologies we are going to include as carriers. Defining carriers is not mandatory but will ease plotting and assigning emissions of CO2 in future steps.
carriers = [
"onwind",
"solar",
"OCGT",
"CCGT",
"battery storage",
]
n.add(
"Carrier",
carriers,
color=["dodgerblue", "gold", "indianred","yellow-green", "brown"],
co2_emissions=[costs.at[c, "CO2 intensity"] for c in carriers],
)
Index(['onwind', 'solar', 'OCGT', 'CCGT', 'battery storage'], dtype='object')
Next, we add the demand time series to the model.
# add load to the bus
n.add("Load",
"demand",
bus="electricity",
p_set=data_el[country].values)
Index(['demand'], dtype='object')
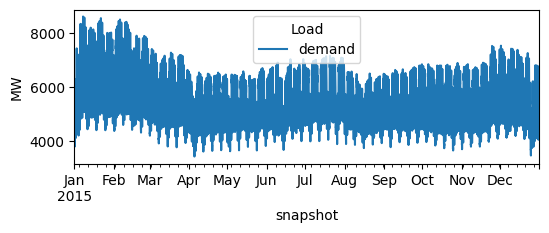
Let’s have a check whether the data was read-in correctly.
n.loads_t.p_set.plot(figsize=(6, 2), ylabel="MW")
<Axes: xlabel='snapshot', ylabel='MW'>
We add now the generators and set up their capacities to be extendable so that they can be optimized together with the dispatch time series. For the wind and solar generator, we need to indicate the capacity factor or maximum power per unit ‘p_max_pu’
n.add(
"Generator",
"OCGT",
bus="electricity",
carrier="OCGT",
capital_cost=costs.at["OCGT", "capital_cost"],
marginal_cost=costs.at["OCGT", "marginal_cost"],
efficiency=costs.at["OCGT", "efficiency"],
p_nom_extendable=True,
)
CF_wind = data_wind[country][[hour.strftime("%Y-%m-%dT%H:%M:%SZ") for hour in n.snapshots]]
n.add(
"Generator",
"onwind",
bus="electricity",
carrier="onwind",
p_max_pu=CF_wind.values,
capital_cost=costs.at["onwind", "capital_cost"],
marginal_cost=costs.at["onwind", "marginal_cost"],
efficiency=costs.at["onwind", "efficiency"],
p_nom_extendable=True,
)
CF_solar = data_solar[country][[hour.strftime("%Y-%m-%dT%H:%M:%SZ") for hour in n.snapshots]]
n.add(
"Generator",
"solar",
bus="electricity",
carrier="solar",
p_max_pu= CF_solar.values,
capital_cost=costs.at["solar", "capital_cost"],
marginal_cost=costs.at["solar", "marginal_cost"],
efficiency=costs.at["solar", "efficiency"],
p_nom_extendable=True,
)
Index(['solar'], dtype='object')
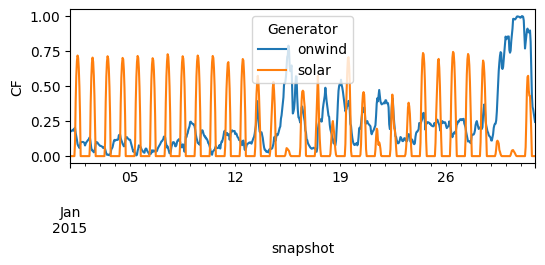
So let’s make sure the capacity factors are read-in correctly.
n.generators_t.p_max_pu.loc["2015-01"].plot(figsize=(6, 2), ylabel="CF")
<Axes: xlabel='snapshot', ylabel='CF'>
We add the battery storage, assuming a fixed energy-to-power ratio of 2 hours, i.e. if fully charged, the battery can discharge at full capacity for 2 hours.
For the capital cost, we have to factor in both the capacity and energy cost of the storage.
We include the charging and discharging efficiencies we enforce a cyclic state-of-charge condition, i.e. the state of charge at the beginning of the optimisation period must equal the final state of charge.
n.add(
"StorageUnit",
"battery storage",
bus="electricity",
carrier="battery storage",
max_hours=2,
capital_cost=costs.at["battery inverter", "capital_cost"]
+ 2 * costs.at["battery storage", "capital_cost"],
efficiency_store=costs.at["battery inverter", "efficiency"],
efficiency_dispatch=costs.at["battery inverter", "efficiency"],
p_nom_extendable=True,
cyclic_state_of_charge=True,
)
Index(['battery storage'], dtype='object')
We add the Combined Cycle Gas Turbine (CCGT). In this case, its capacity is not extendable but fixed to 1 GW.
n.add(
"Generator",
"CCGT",
bus="electricity",
carrier="CCGT",
capital_cost=costs.at["CCGT", "capital_cost"],
marginal_cost=costs.at["CCGT", "marginal_cost"],
efficiency=costs.at["CCGT", "efficiency"],
p_nom=6000, #6 Gw
)
Index(['CCGT'], dtype='object')
Model Run#
We can already solved the model using the open-solver “highs” or the commercial solver “gurobi” with the academic license
n.optimize(solver_name="highs")
WARNING:pypsa.consistency:The following buses have carriers which are not defined:
Index(['electricity'], dtype='object', name='Bus')
INFO:linopy.model: Solve problem using Highs solver
INFO:linopy.io:Writing objective.
Writing constraints.: 0%| | 0/16 [00:00<?, ?it/s]
Writing constraints.: 44%|████▍ | 7/16 [00:00<00:00, 52.64it/s]
Writing constraints.: 81%|████████▏ | 13/16 [00:00<00:00, 30.47it/s]
Writing constraints.: 100%|██████████| 16/16 [00:00<00:00, 26.46it/s]
Writing continuous variables.: 0%| | 0/6 [00:00<?, ?it/s]
Writing continuous variables.: 100%|██████████| 6/6 [00:00<00:00, 57.65it/s]
Writing continuous variables.: 100%|██████████| 6/6 [00:00<00:00, 57.31it/s]
INFO:linopy.io: Writing time: 0.77s
Running HiGHS 1.10.0 (git hash: fd86653): Copyright (c) 2025 HiGHS under MIT licence terms
LP linopy-problem-wrds25an has 140164 rows; 61324 cols; 258442 nonzeros
Coefficient ranges:
Matrix [1e-03, 2e+00]
Cost [1e-02, 1e+05]
Bound [0e+00, 0e+00]
RHS [3e+03, 9e+03]
Presolving model
65718 rows, 56962 cols, 179634 nonzeros 0s
Dependent equations search running on 17520 equations with time limit of 1000.00s
Dependent equations search removed 0 rows and 0 nonzeros in 0.00s (limit = 1000.00s)
65718 rows, 56962 cols, 179634 nonzeros 0s
Presolve : Reductions: rows 65718(-74446); columns 56962(-4362); elements 179634(-78808)
Solving the presolved LP
Using EKK dual simplex solver - serial
Iteration Objective Infeasibilities num(sum)
0 0.0000000000e+00 Pr: 8760(1.56078e+09) 0s
54458 2.1992090699e+09 Pr: 4596(3.63438e+09); Du: 0(2.90985e-07) 5s
66113 2.2612394444e+09 Pr: 0(0); Du: 0(2.64582e-14) 7s
66113 2.2612394444e+09 Pr: 0(0); Du: 0(2.64582e-14) 7s
Solving the original LP from the solution after postsolve
Model name : linopy-problem-wrds25an
Model status : Optimal
Simplex iterations: 66113
Objective value : 2.2612394444e+09
Relative P-D gap : 1.0543712197e-15
HiGHS run time : 7.16
INFO:linopy.constants: Optimization successful:
Status: ok
Termination condition: optimal
Solution: 61324 primals, 140164 duals
Objective: 2.26e+09
Solver model: available
Solver message: Optimal
INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Generator-ext-p-lower, Generator-ext-p-upper, StorageUnit-ext-p_dispatch-lower, StorageUnit-ext-p_dispatch-upper, StorageUnit-ext-p_store-lower, StorageUnit-ext-p_store-upper, StorageUnit-ext-state_of_charge-lower, StorageUnit-ext-state_of_charge-upper, StorageUnit-energy_balance were not assigned to the network.
Writing the solution to /tmp/linopy-solve-9k2ie0w0.sol
('ok', 'optimal')
Now, we can look at the results and evaluate the total system cost (in billion Euros per year)
n.objective / 1e9
2.2612394444437998
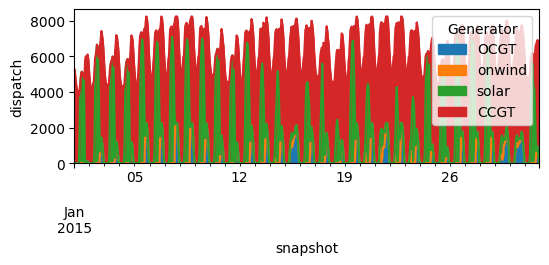
The optimised capacities in GW:
n.generators.p_nom_opt.div(1e3) # MW -> GW
Generator
OCGT 2.252259
onwind -0.000000
solar 9.761450
CCGT 6.000000
Name: p_nom_opt, dtype: float64
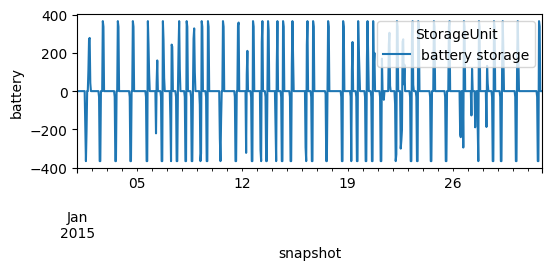
The optimised battery capacity can be calcualted as
n.storage_units.p_nom_opt.div(1e3) # MW -> GW
StorageUnit
battery storage 0.365741
Name: p_nom_opt, dtype: float64
The total energy generation by technology in TWh:
n.generators_t.p.sum().div(1e6) # MWh -> TWh
Generator
OCGT 0.714574
onwind 0.000000
solar 14.312445
CCGT 33.921320
dtype: float64
We can plot the dispatch of every generator thoughout January
n.generators_t.p.loc["2015-01"].plot.area(figsize=(6, 2), ylabel="dispatch")
<Axes: xlabel='snapshot', ylabel='dispatch'>
We can also plot the charging and discharging of the battery
n.storage_units_t.p.loc["2015-01"].plot(figsize=(6, 2), ylabel="battery")
<Axes: xlabel='snapshot', ylabel='battery'>
and the demand time series
n.loads_t.p.loc["2015-01"].plot(figsize=(6, 2), ylabel="demand")
<Axes: xlabel='snapshot', ylabel='demand'>
b) How does the CCGT power plant recover its cost?
To calculate the revenues collected by every technology, for every generator, we multiply the energy generated in very hour by the electricity price in that hour and sum for the entire year.
n.generators_t.p.multiply(n.buses_t.marginal_price.to_numpy()).sum().div(1e6) # EUR -> MEUR
Generator
OCGT 153.696309
onwind 0.000000
solar 501.371243
CCGT 1988.635424
dtype: float64
This corresponds to the total cost for every technology, which we can also read using the statistics module:
(n.statistics.capex() + n.statistics.opex()).div(1e6)
component carrier
Generator CCGT 2216.351778
OCGT 153.696309
solar 501.371243
StorageUnit battery storage NaN
dtype: float64
The CCGT does not recover its full cost. This is to be expected because its capacity was not optimized but set exogenously
c) How does the battery recover its cost?
The battery capacity is also co-optimized with the dispatch, so it exactly recovers its cost by buying electricity when the price is low and selling when it is high. The revenues from market can be calculated by multiplying the battery charging and discharging by the electricity price time series
n.storage_units_t.p.multiply(n.buses_t.marginal_price.to_numpy()).sum().div(1e6) # EUR -> MEUR
StorageUnit
battery storage 18.548238
dtype: float64
The market revenues exactly correspons with the total battery costs
n.storage_units.p_nom_opt*(costs.at["battery inverter", "capital_cost"]+ 2 * costs.at["battery storage", "capital_cost"])/(1e6)# EUR -> MEUR
StorageUnit
battery storage 18.548238
Name: p_nom_opt, dtype: float64

