Course project#
This notebook includes the steps to optimize the capacity and dispatch of generators in a stylized energy system. It has been prepared to serve as a tutorial for a simple PyPSA model representing the energy system in one country, city or region.
For the (optional) project of the course Integrated Energy Grids you need to deliver a report including the sections described at the end of this notebook.
Please, review the PyPSA tutorial before starting this project.
Note
If you have not yet set up Python on your computer, you can execute this tutorial in your browser via Google Colab. Click on the rocket in the top right corner and launch “Colab”. If that doesn’t work download the .ipynb file and import it in Google Colab.
Then install pandas and pypsa by executing the following command in a Jupyter cell at the top of the notebook.
!pip install pandas pypsa
import pandas as pd
import pypsa
We start by creating the network. In this example, the country is modelled as a single node, so the network includes only one bus.
We select the year 2015 and set the hours in that year as snapshots.
We select a country, in this case Denmark (DNK), and add one node (electricity bus) to the network.
network = pypsa.Network()
hours_in_2015 = pd.date_range('2015-01-01 00:00Z',
'2015-12-31 23:00Z',
freq='h')
network.set_snapshots(hours_in_2015.values)
network.add("Bus",
"electricity bus")
network.snapshots
DatetimeIndex(['2015-01-01 00:00:00', '2015-01-01 01:00:00',
'2015-01-01 02:00:00', '2015-01-01 03:00:00',
'2015-01-01 04:00:00', '2015-01-01 05:00:00',
'2015-01-01 06:00:00', '2015-01-01 07:00:00',
'2015-01-01 08:00:00', '2015-01-01 09:00:00',
...
'2015-12-31 14:00:00', '2015-12-31 15:00:00',
'2015-12-31 16:00:00', '2015-12-31 17:00:00',
'2015-12-31 18:00:00', '2015-12-31 19:00:00',
'2015-12-31 20:00:00', '2015-12-31 21:00:00',
'2015-12-31 22:00:00', '2015-12-31 23:00:00'],
dtype='datetime64[ns]', name='snapshot', length=8760, freq=None)
The demand is represented by the historical electricity demand in 2015 with hourly resolution.
The file with historical hourly electricity demand for every European country is available in the data folder.
The electricity demand time series were obtained from ENTSOE through the very convenient compilation carried out by the Open Power System Data (OPSD). https://data.open-power-system-data.org/time_series/
# load electricity demand data
df_elec = pd.read_csv('data/electricity_demand.csv', sep=';', index_col=0) # in MWh
df_elec.index = pd.to_datetime(df_elec.index) #change index to datatime
country='DNK'
print(df_elec[country].head())
utc_time
2015-01-01 00:00:00+00:00 3210.98
2015-01-01 01:00:00+00:00 3100.02
2015-01-01 02:00:00+00:00 2980.39
2015-01-01 03:00:00+00:00 2933.49
2015-01-01 04:00:00+00:00 2941.54
Name: DNK, dtype: float64
# add load to the bus
network.add("Load",
"load",
bus="electricity bus",
p_set=df_elec[country].values)
Index(['load'], dtype='object')
Print the load time series to check that it has been properly added (you should see numbers and not ‘NaN’)
network.loads_t.p_set
| Load | load |
|---|---|
| snapshot | |
| 2015-01-01 00:00:00 | 3210.98 |
| 2015-01-01 01:00:00 | 3100.02 |
| 2015-01-01 02:00:00 | 2980.39 |
| 2015-01-01 03:00:00 | 2933.49 |
| 2015-01-01 04:00:00 | 2941.54 |
| ... | ... |
| 2015-12-31 19:00:00 | 3687.87 |
| 2015-12-31 20:00:00 | 3535.55 |
| 2015-12-31 21:00:00 | 3389.26 |
| 2015-12-31 22:00:00 | 3262.27 |
| 2015-12-31 23:00:00 | 3158.85 |
8760 rows × 1 columns
In the optimization, we will minimize the annualized system costs.
We will need to annualize the cost of every generator, we build a function to do it.
def annuity(n,r):
""" Calculate the annuity factor for an asset with lifetime n years and
discount rate r """
if r > 0:
return r/(1. - 1./(1.+r)**n)
else:
return 1/n
We include solar PV and onshore wind generators.
The capacity factors representing the availability of those generators for every European country can be downloaded from the following repositories (select ‘optimal’ for PV and onshore for wind).
https://zenodo.org/record/3253876#.XSiVOEdS8l0
https://zenodo.org/record/2613651#.XSiVOkdS8l0
We include also Open Cycle Gas Turbine (OCGT) generators
The cost assumed for the generators are the same as in Table 1 in the paper https://doi.org/10.1016/j.enconman.2019.111977 (open version: https://arxiv.org/pdf/1906.06936.pdf)
# add the different carriers, only gas emits CO2
network.add("Carrier", "gas", co2_emissions=0.19) # in t_CO2/MWh_th
network.add("Carrier", "onshorewind")
network.add("Carrier", "solar")
# add onshore wind generator
df_onshorewind = pd.read_csv('data/onshore_wind_1979-2017.csv', sep=';', index_col=0)
df_onshorewind.index = pd.to_datetime(df_onshorewind.index)
CF_wind = df_onshorewind[country][[hour.strftime("%Y-%m-%dT%H:%M:%SZ") for hour in network.snapshots]]
capital_cost_onshorewind = annuity(30,0.07)*910000*(1+0.033) # in €/MW
network.add("Generator",
"onshorewind",
bus="electricity bus",
p_nom_extendable=True,
carrier="onshorewind",
#p_nom_max=1000, # maximum capacity can be limited due to environmental constraints
capital_cost = capital_cost_onshorewind,
marginal_cost = 0,
p_max_pu = CF_wind.values)
# add solar PV generator
df_solar = pd.read_csv('data/pv_optimal.csv', sep=';', index_col=0)
df_solar.index = pd.to_datetime(df_solar.index)
CF_solar = df_solar[country][[hour.strftime("%Y-%m-%dT%H:%M:%SZ") for hour in network.snapshots]]
capital_cost_solar = annuity(25,0.07)*425000*(1+0.03) # in €/MW
network.add("Generator",
"solar",
bus="electricity bus",
p_nom_extendable=True,
carrier="solar",
#p_nom_max=1000, # maximum capacity can be limited due to environmental constraints
capital_cost = capital_cost_solar,
marginal_cost = 0,
p_max_pu = CF_solar.values)
# add OCGT (Open Cycle Gas Turbine) generator
capital_cost_OCGT = annuity(25,0.07)*560000*(1+0.033) # in €/MW
fuel_cost = 21.6 # in €/MWh_th
efficiency = 0.39 # MWh_elec/MWh_th
marginal_cost_OCGT = fuel_cost/efficiency # in €/MWh_el
network.add("Generator",
"OCGT",
bus="electricity bus",
p_nom_extendable=True,
carrier="gas",
#p_nom_max=1000,
capital_cost = capital_cost_OCGT,
marginal_cost = marginal_cost_OCGT)
Index(['OCGT'], dtype='object')
Print the generator Capacity factor time series to check that it has been properly added (you should see numbers and not ‘NaN’)
network.generators_t.p_max_pu
| Generator | onshorewind | solar |
|---|---|---|
| snapshot | ||
| 2015-01-01 00:00:00 | 0.460 | 0.0 |
| 2015-01-01 01:00:00 | 0.465 | 0.0 |
| 2015-01-01 02:00:00 | 0.478 | 0.0 |
| 2015-01-01 03:00:00 | 0.548 | 0.0 |
| 2015-01-01 04:00:00 | 0.593 | 0.0 |
| ... | ... | ... |
| 2015-12-31 19:00:00 | 0.174 | 0.0 |
| 2015-12-31 20:00:00 | 0.145 | 0.0 |
| 2015-12-31 21:00:00 | 0.141 | 0.0 |
| 2015-12-31 22:00:00 | 0.164 | 0.0 |
| 2015-12-31 23:00:00 | 0.204 | 0.0 |
8760 rows × 2 columns
We find the optimal solution using Gurobi as solver.
In this case, we are optimizing the installed capacity and dispatch of every generator to minimize the total system cost.
network.optimize(solver_name='gurobi')
WARNING:pypsa.consistency:The following buses have carriers which are not defined:
Index(['electricity bus'], dtype='object', name='Bus')
INFO:linopy.model: Solve problem using Gurobi solver
INFO:linopy.io:Writing objective.
Writing constraints.: 0%| | 0/5 [00:00<?, ?it/s]
Writing constraints.: 80%|████████ | 4/5 [00:00<00:00, 21.12it/s]
Writing constraints.: 100%|██████████| 5/5 [00:00<00:00, 20.48it/s]
Writing continuous variables.: 0%| | 0/2 [00:00<?, ?it/s]
Writing continuous variables.: 100%|██████████| 2/2 [00:00<00:00, 44.58it/s]
INFO:linopy.io: Writing time: 0.31s
Restricted license - for non-production use only - expires 2026-11-23
INFO:gurobipy:Restricted license - for non-production use only - expires 2026-11-23
Read LP format model from file /tmp/linopy-problem-lopzzep_.lp
INFO:gurobipy:Read LP format model from file /tmp/linopy-problem-lopzzep_.lp
Reading time = 0.07 seconds
INFO:gurobipy:Reading time = 0.07 seconds
obj: 61323 rows, 26283 columns, 100750 nonzeros
INFO:gurobipy:obj: 61323 rows, 26283 columns, 100750 nonzeros
Gurobi Optimizer version 12.0.2 build v12.0.2rc0 (linux64 - "Ubuntu 24.04.2 LTS")
INFO:gurobipy:Gurobi Optimizer version 12.0.2 build v12.0.2rc0 (linux64 - "Ubuntu 24.04.2 LTS")
INFO:gurobipy:
CPU model: AMD EPYC 7763 64-Core Processor, instruction set [SSE2|AVX|AVX2]
INFO:gurobipy:CPU model: AMD EPYC 7763 64-Core Processor, instruction set [SSE2|AVX|AVX2]
Thread count: 2 physical cores, 4 logical processors, using up to 4 threads
INFO:gurobipy:Thread count: 2 physical cores, 4 logical processors, using up to 4 threads
INFO:gurobipy:
---------------------------------------------------------------------------
GurobiError Traceback (most recent call last)
Cell In[9], line 1
----> 1 network.optimize(solver_name='gurobi')
File /opt/hostedtoolcache/Python/3.11.12/x64/lib/python3.11/site-packages/pypsa/optimization/optimize.py:633, in OptimizationAccessor.__call__(self, *args, **kwargs)
631 @wraps(optimize)
632 def __call__(self, *args: Any, **kwargs: Any) -> Any:
--> 633 return optimize(self.n, *args, **kwargs)
File /opt/hostedtoolcache/Python/3.11.12/x64/lib/python3.11/site-packages/pypsa/optimization/optimize.py:605, in optimize(n, snapshots, multi_investment_periods, transmission_losses, linearized_unit_commitment, model_kwargs, extra_functionality, assign_all_duals, solver_name, solver_options, compute_infeasibilities, **kwargs)
603 if extra_functionality:
604 extra_functionality(n, sns)
--> 605 status, condition = m.solve(solver_name=solver_name, **solver_options, **kwargs)
607 if status == "ok":
608 assign_solution(n)
File /opt/hostedtoolcache/Python/3.11.12/x64/lib/python3.11/site-packages/linopy/model.py:1206, in Model.solve(self, solver_name, io_api, explicit_coordinate_names, problem_fn, solution_fn, log_fn, basis_fn, warmstart_fn, keep_files, env, sanitize_zeros, sanitize_infinities, slice_size, remote, progress, **solver_options)
1198 explicit_coordinate_names = False
1199 problem_fn = self.to_file(
1200 to_path(problem_fn),
1201 io_api=io_api,
(...) 1204 progress=progress,
1205 )
-> 1206 result = solver.solve_problem_from_file(
1207 problem_fn=to_path(problem_fn),
1208 solution_fn=to_path(solution_fn),
1209 log_fn=to_path(log_fn),
1210 warmstart_fn=to_path(warmstart_fn),
1211 basis_fn=to_path(basis_fn),
1212 env=env,
1213 )
1215 finally:
1216 for fn in (problem_fn, solution_fn):
File /opt/hostedtoolcache/Python/3.11.12/x64/lib/python3.11/site-packages/linopy/solvers.py:1039, in Gurobi.solve_problem_from_file(self, problem_fn, solution_fn, log_fn, warmstart_fn, basis_fn, env)
1035 env_ = env
1037 m = gurobipy.read(problem_fn_, env=env_)
-> 1039 return self._solve(
1040 m,
1041 solution_fn=solution_fn,
1042 log_fn=log_fn,
1043 warmstart_fn=warmstart_fn,
1044 basis_fn=basis_fn,
1045 io_api=io_api,
1046 sense=sense,
1047 )
File /opt/hostedtoolcache/Python/3.11.12/x64/lib/python3.11/site-packages/linopy/solvers.py:1113, in Gurobi._solve(self, m, solution_fn, log_fn, warmstart_fn, basis_fn, io_api, sense)
1111 if warmstart_fn is not None:
1112 m.read(path_to_string(warmstart_fn))
-> 1113 m.optimize()
1115 if basis_fn is not None:
1116 try:
File src/gurobipy/_model.pyx:903, in gurobipy._model.Model.optimize()
GurobiError: Model too large for size-limited license; visit https://gurobi.com/unrestricted for more information
The message (‘ok’ , ‘optimal”) indicates that the optimizer has found an optimal solution.
The total cost can be read from the network objetive.
print(network.objective/1000000) #in 10^6 €
1699.4058099821536
The cost per MWh of electricity produced can also be calculated.
print(network.objective/network.loads_t.p.sum()) # EUR/MWh
Load
load 51.789144
dtype: float64
The optimal capacity for every generator can be shown.
network.generators.p_nom_opt # in MW
Generator
onshorewind 7010.549199
solar 2871.404793
OCGT 5405.382311
Name: p_nom_opt, dtype: float64
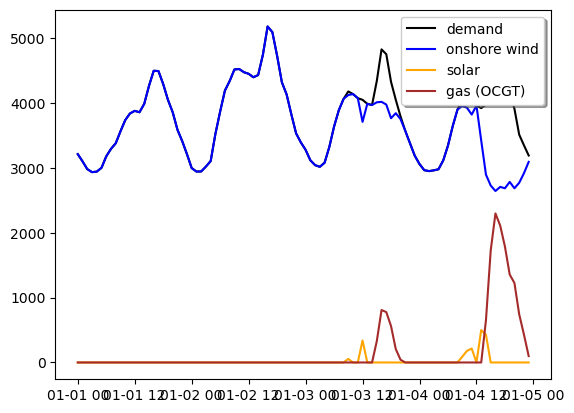
We can plot now the dispatch of every generator during the first week of the year and the electricity demand. We import the matplotlib package which is very useful to plot results.
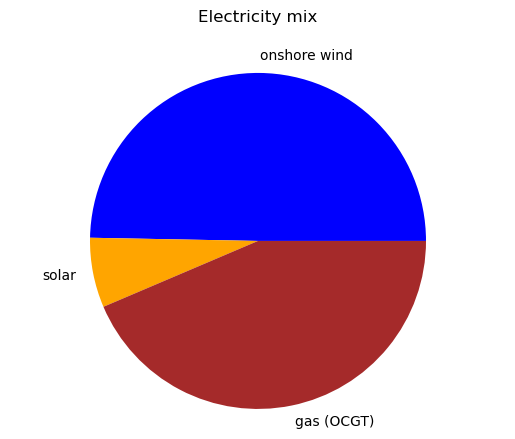
We can also plot the electricity mix.
import matplotlib.pyplot as plt
plt.plot(network.loads_t.p['load'][0:96], color='black', label='demand')
plt.plot(network.generators_t.p['onshorewind'][0:96], color='blue', label='onshore wind')
plt.plot(network.generators_t.p['solar'][0:96], color='orange', label='solar')
plt.plot(network.generators_t.p['OCGT'][0:96], color='brown', label='gas (OCGT)')
plt.legend(fancybox=True, shadow=True, loc='best')
<matplotlib.legend.Legend at 0x279e62ca1e0>
labels = ['onshore wind',
'solar',
'gas (OCGT)']
sizes = [network.generators_t.p['onshorewind'].sum(),
network.generators_t.p['solar'].sum(),
network.generators_t.p['OCGT'].sum()]
colors=['blue', 'orange', 'brown']
plt.pie(sizes,
colors=colors,
labels=labels,
wedgeprops={'linewidth':0})
plt.axis('equal')
plt.title('Electricity mix', y=1.07)
Text(0.5, 1.07, 'Electricity mix')
We can add a global CO2 constraint and solve again.
co2_limit=1000000 #tonCO2
network.add("GlobalConstraint",
"co2_limit",
type="primary_energy",
carrier_attribute="co2_emissions",
sense="<=",
constant=co2_limit)
network.optimize(solver_name='gurobi')
WARNING:pypsa.consistency:The following buses have carriers which are not defined:
Index(['electricity bus'], dtype='object', name='Bus')
WARNING:pypsa.consistency:The following buses have carriers which are not defined:
Index(['electricity bus'], dtype='object', name='Bus')
INFO:linopy.model: Solve problem using Gurobi solver
INFO:linopy.io:Writing objective.
Writing constraints.: 100%|██████████| 6/6 [00:00<00:00, 13.44it/s]
Writing continuous variables.: 100%|██████████| 2/2 [00:00<00:00, 17.86it/s]
INFO:linopy.io: Writing time: 0.59s
Set parameter Username
INFO:gurobipy:Set parameter Username
Set parameter LicenseID to value 2604332
INFO:gurobipy:Set parameter LicenseID to value 2604332
Academic license - for non-commercial use only - expires 2025-12-30
INFO:gurobipy:Academic license - for non-commercial use only - expires 2025-12-30
Read LP format model from file C:\Users\34620\AppData\Local\Temp\linopy-problem-s0u80xfl.lp
INFO:gurobipy:Read LP format model from file C:\Users\34620\AppData\Local\Temp\linopy-problem-s0u80xfl.lp
Reading time = 0.15 seconds
INFO:gurobipy:Reading time = 0.15 seconds
obj: 61324 rows, 26283 columns, 109510 nonzeros
INFO:gurobipy:obj: 61324 rows, 26283 columns, 109510 nonzeros
Gurobi Optimizer version 12.0.0 build v12.0.0rc1 (win64 - Windows 11.0 (26100.2))
INFO:gurobipy:Gurobi Optimizer version 12.0.0 build v12.0.0rc1 (win64 - Windows 11.0 (26100.2))
INFO:gurobipy:
CPU model: Intel(R) Core(TM) i7-8550U CPU @ 1.80GHz, instruction set [SSE2|AVX|AVX2]
INFO:gurobipy:CPU model: Intel(R) Core(TM) i7-8550U CPU @ 1.80GHz, instruction set [SSE2|AVX|AVX2]
Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
INFO:gurobipy:Thread count: 4 physical cores, 8 logical processors, using up to 8 threads
INFO:gurobipy:
Optimize a model with 61324 rows, 26283 columns and 109510 nonzeros
INFO:gurobipy:Optimize a model with 61324 rows, 26283 columns and 109510 nonzeros
Model fingerprint: 0x985d7065
INFO:gurobipy:Model fingerprint: 0x985d7065
Coefficient statistics:
INFO:gurobipy:Coefficient statistics:
Matrix range [1e-03, 1e+00]
INFO:gurobipy: Matrix range [1e-03, 1e+00]
Objective range [6e+01, 8e+04]
INFO:gurobipy: Objective range [6e+01, 8e+04]
Bounds range [0e+00, 0e+00]
INFO:gurobipy: Bounds range [0e+00, 0e+00]
RHS range [2e+03, 1e+06]
INFO:gurobipy: RHS range [2e+03, 1e+06]
Presolve removed 35029 rows and 8746 columns
INFO:gurobipy:Presolve removed 35029 rows and 8746 columns
Presolve time: 0.15s
INFO:gurobipy:Presolve time: 0.15s
Presolved: 26295 rows, 17537 columns, 65735 nonzeros
INFO:gurobipy:Presolved: 26295 rows, 17537 columns, 65735 nonzeros
INFO:gurobipy:
Concurrent LP optimizer: dual simplex and barrier
INFO:gurobipy:Concurrent LP optimizer: dual simplex and barrier
Showing barrier log only...
INFO:gurobipy:Showing barrier log only...
INFO:gurobipy:
Ordering time: 0.01s
INFO:gurobipy:Ordering time: 0.01s
INFO:gurobipy:
Barrier statistics:
INFO:gurobipy:Barrier statistics:
Dense cols : 3
INFO:gurobipy: Dense cols : 3
AA' NZ : 5.696e+04
INFO:gurobipy: AA' NZ : 5.696e+04
Factor NZ : 1.536e+05 (roughly 20 MB of memory)
INFO:gurobipy: Factor NZ : 1.536e+05 (roughly 20 MB of memory)
Factor Ops : 9.458e+05 (less than 1 second per iteration)
INFO:gurobipy: Factor Ops : 9.458e+05 (less than 1 second per iteration)
Threads : 1
INFO:gurobipy: Threads : 1
INFO:gurobipy:
Objective Residual
INFO:gurobipy: Objective Residual
Iter Primal Dual Primal Dual Compl Time
INFO:gurobipy:Iter Primal Dual Primal Dual Compl Time
0 2.94119004e+11 -1.11451635e+11 4.49e+07 0.00e+00 1.02e+09 0s
INFO:gurobipy: 0 2.94119004e+11 -1.11451635e+11 4.49e+07 0.00e+00 1.02e+09 0s
1 5.33634949e+11 -1.53566777e+11 4.86e+06 2.13e+02 1.43e+08 0s
INFO:gurobipy: 1 5.33634949e+11 -1.53566777e+11 4.86e+06 2.13e+02 1.43e+08 0s
2 3.71030736e+11 -1.46538231e+11 1.26e+05 7.20e-10 1.05e+07 0s
INFO:gurobipy: 2 3.71030736e+11 -1.46538231e+11 1.26e+05 7.20e-10 1.05e+07 0s
3 6.16870731e+10 -5.84407747e+10 1.73e+04 1.05e-09 2.20e+06 0s
INFO:gurobipy: 3 6.16870731e+10 -5.84407747e+10 1.73e+04 1.05e-09 2.20e+06 0s
4 5.08966419e+10 -5.10672255e+10 1.39e+04 8.26e-10 1.86e+06 0s
INFO:gurobipy: 4 5.08966419e+10 -5.10672255e+10 1.39e+04 8.26e-10 1.86e+06 0s
5 2.25693425e+10 -3.00006735e+10 4.85e+03 1.44e-09 9.39e+05 0s
INFO:gurobipy: 5 2.25693425e+10 -3.00006735e+10 4.85e+03 1.44e-09 9.39e+05 0s
6 1.63203080e+10 -1.89676442e+10 3.11e+03 6.29e-10 6.27e+05 0s
INFO:gurobipy: 6 1.63203080e+10 -1.89676442e+10 3.11e+03 6.29e-10 6.27e+05 0s
7 9.31801285e+09 -1.09558254e+10 1.29e+03 7.17e-10 3.58e+05 0s
INFO:gurobipy: 7 9.31801285e+09 -1.09558254e+10 1.29e+03 7.17e-10 3.58e+05 0s
8 6.95861133e+09 -8.61403926e+09 7.48e+02 5.46e-11 2.75e+05 0s
INFO:gurobipy: 8 6.95861133e+09 -8.61403926e+09 7.48e+02 5.46e-11 2.75e+05 0s
9 5.90046566e+09 -4.47912849e+09 5.46e+02 4.65e-10 1.83e+05 0s
INFO:gurobipy: 9 5.90046566e+09 -4.47912849e+09 5.46e+02 4.65e-10 1.83e+05 0s
10 5.02948120e+09 -1.77188711e+09 4.14e+02 1.30e-10 1.20e+05 0s
INFO:gurobipy: 10 5.02948120e+09 -1.77188711e+09 4.14e+02 1.30e-10 1.20e+05 0s
11 4.50201254e+09 -1.30587343e+09 3.32e+02 3.07e-10 1.02e+05 0s
INFO:gurobipy: 11 4.50201254e+09 -1.30587343e+09 3.32e+02 3.07e-10 1.02e+05 0s
12 3.95933836e+09 -7.66635420e+08 2.58e+02 3.15e-10 8.32e+04 1s
INFO:gurobipy: 12 3.95933836e+09 -7.66635420e+08 2.58e+02 3.15e-10 8.32e+04 1s
13 3.61608472e+09 3.47505627e+08 2.03e+02 6.75e-14 5.76e+04 1s
INFO:gurobipy: 13 3.61608472e+09 3.47505627e+08 2.03e+02 6.75e-14 5.76e+04 1s
14 3.39761330e+09 5.37286458e+08 1.72e+02 2.95e-10 5.04e+04 1s
INFO:gurobipy: 14 3.39761330e+09 5.37286458e+08 1.72e+02 2.95e-10 5.04e+04 1s
15 3.18459805e+09 1.10818850e+09 1.42e+02 4.63e-10 3.66e+04 1s
INFO:gurobipy: 15 3.18459805e+09 1.10818850e+09 1.42e+02 4.63e-10 3.66e+04 1s
16 2.94747283e+09 1.42691087e+09 1.05e+02 1.08e-10 2.68e+04 1s
INFO:gurobipy: 16 2.94747283e+09 1.42691087e+09 1.05e+02 1.08e-10 2.68e+04 1s
17 2.78443852e+09 1.67783788e+09 7.72e+01 1.94e-10 1.95e+04 1s
INFO:gurobipy: 17 2.78443852e+09 1.67783788e+09 7.72e+01 1.94e-10 1.95e+04 1s
18 2.68794375e+09 1.81199310e+09 6.15e+01 5.29e-10 1.54e+04 1s
INFO:gurobipy: 18 2.68794375e+09 1.81199310e+09 6.15e+01 5.29e-10 1.54e+04 1s
19 2.61234531e+09 1.95343943e+09 4.82e+01 5.33e-14 1.16e+04 1s
INFO:gurobipy: 19 2.61234531e+09 1.95343943e+09 4.82e+01 5.33e-14 1.16e+04 1s
20 2.55185932e+09 2.06355566e+09 3.74e+01 2.36e-10 8.60e+03 1s
INFO:gurobipy: 20 2.55185932e+09 2.06355566e+09 3.74e+01 2.36e-10 8.60e+03 1s
21 2.51217334e+09 2.13702686e+09 2.93e+01 1.16e-10 6.61e+03 1s
INFO:gurobipy: 21 2.51217334e+09 2.13702686e+09 2.93e+01 1.16e-10 6.61e+03 1s
22 2.49097303e+09 2.19740759e+09 2.55e+01 3.71e-10 5.17e+03 1s
INFO:gurobipy: 22 2.49097303e+09 2.19740759e+09 2.55e+01 3.71e-10 5.17e+03 1s
23 2.46855656e+09 2.24076505e+09 2.08e+01 6.52e-10 4.01e+03 1s
INFO:gurobipy: 23 2.46855656e+09 2.24076505e+09 2.08e+01 6.52e-10 4.01e+03 1s
24 2.42512256e+09 2.26502741e+09 1.15e+01 9.65e-14 2.82e+03 1s
INFO:gurobipy: 24 2.42512256e+09 2.26502741e+09 1.15e+01 9.65e-14 2.82e+03 1s
25 2.40616534e+09 2.29949405e+09 7.53e+00 6.81e-13 1.88e+03 1s
INFO:gurobipy: 25 2.40616534e+09 2.29949405e+09 7.53e+00 6.81e-13 1.88e+03 1s
26 2.39551855e+09 2.31735585e+09 5.34e+00 3.08e-10 1.38e+03 1s
INFO:gurobipy: 26 2.39551855e+09 2.31735585e+09 5.34e+00 3.08e-10 1.38e+03 1s
27 2.38887715e+09 2.32269809e+09 4.04e+00 1.48e-11 1.16e+03 1s
INFO:gurobipy: 27 2.38887715e+09 2.32269809e+09 4.04e+00 1.48e-11 1.16e+03 1s
28 2.38711106e+09 2.32718049e+09 3.69e+00 6.90e-10 1.05e+03 1s
INFO:gurobipy: 28 2.38711106e+09 2.32718049e+09 3.69e+00 6.90e-10 1.05e+03 1s
29 2.37843114e+09 2.33290536e+09 1.73e+00 3.89e-10 8.00e+02 1s
INFO:gurobipy: 29 2.37843114e+09 2.33290536e+09 1.73e+00 3.89e-10 8.00e+02 1s
30 2.37530087e+09 2.34558289e+09 1.19e+00 3.75e-10 5.23e+02 1s
INFO:gurobipy: 30 2.37530087e+09 2.34558289e+09 1.19e+00 3.75e-10 5.23e+02 1s
31 2.37139601e+09 2.34991112e+09 6.19e-01 2.41e-10 3.78e+02 1s
INFO:gurobipy: 31 2.37139601e+09 2.34991112e+09 6.19e-01 2.41e-10 3.78e+02 1s
32 2.37067269e+09 2.35123788e+09 4.72e-01 5.17e-10 3.42e+02 1s
INFO:gurobipy: 32 2.37067269e+09 2.35123788e+09 4.72e-01 5.17e-10 3.42e+02 1s
33 2.37036798e+09 2.35323691e+09 4.24e-01 4.72e-10 3.01e+02 1s
INFO:gurobipy: 33 2.37036798e+09 2.35323691e+09 4.24e-01 4.72e-10 3.01e+02 1s
34 2.36922899e+09 2.35749118e+09 2.48e-01 2.72e-10 2.06e+02 1s
INFO:gurobipy: 34 2.36922899e+09 2.35749118e+09 2.48e-01 2.72e-10 2.06e+02 1s
35 2.36905260e+09 2.35886492e+09 2.27e-01 1.85e-10 1.79e+02 1s
INFO:gurobipy: 35 2.36905260e+09 2.35886492e+09 2.27e-01 1.85e-10 1.79e+02 1s
36 2.36819216e+09 2.36099671e+09 8.77e-02 3.33e-10 1.26e+02 1s
INFO:gurobipy: 36 2.36819216e+09 2.36099671e+09 8.77e-02 3.33e-10 1.26e+02 1s
37 2.36780558e+09 2.36153934e+09 5.64e-02 3.47e-10 1.10e+02 1s
INFO:gurobipy: 37 2.36780558e+09 2.36153934e+09 5.64e-02 3.47e-10 1.10e+02 1s
38 2.36768197e+09 2.36367083e+09 4.29e-02 3.79e-10 7.05e+01 1s
INFO:gurobipy: 38 2.36768197e+09 2.36367083e+09 4.29e-02 3.79e-10 7.05e+01 1s
39 2.36744955e+09 2.36518750e+09 2.43e-02 1.85e-10 3.97e+01 1s
INFO:gurobipy: 39 2.36744955e+09 2.36518750e+09 2.43e-02 1.85e-10 3.97e+01 1s
40 2.36736254e+09 2.36561000e+09 1.78e-02 4.16e-10 3.08e+01 1s
INFO:gurobipy: 40 2.36736254e+09 2.36561000e+09 1.78e-02 4.16e-10 3.08e+01 1s
41 2.36726249e+09 2.36607289e+09 1.02e-02 1.21e-10 2.09e+01 1s
INFO:gurobipy: 41 2.36726249e+09 2.36607289e+09 1.02e-02 1.21e-10 2.09e+01 1s
42 2.36717325e+09 2.36649479e+09 1.80e-03 1.43e-10 1.19e+01 1s
INFO:gurobipy: 42 2.36717325e+09 2.36649479e+09 1.80e-03 1.43e-10 1.19e+01 1s
43 2.36715257e+09 2.36666615e+09 9.92e-04 1.14e-10 8.54e+00 1s
INFO:gurobipy: 43 2.36715257e+09 2.36666615e+09 9.92e-04 1.14e-10 8.54e+00 1s
44 2.36712257e+09 2.36712165e+09 4.03e-08 2.06e-11 1.61e-02 1s
INFO:gurobipy: 44 2.36712257e+09 2.36712165e+09 4.03e-08 2.06e-11 1.61e-02 1s
45 2.36712251e+09 2.36712251e+09 6.50e-08 1.11e-08 2.46e-08 1s
INFO:gurobipy: 45 2.36712251e+09 2.36712251e+09 6.50e-08 1.11e-08 2.46e-08 1s
46 2.36712251e+09 2.36712251e+09 4.64e-11 1.11e-08 2.46e-14 1s
INFO:gurobipy: 46 2.36712251e+09 2.36712251e+09 4.64e-11 1.11e-08 2.46e-14 1s
INFO:gurobipy:
Barrier solved model in 46 iterations and 1.31 seconds (0.45 work units)
INFO:gurobipy:Barrier solved model in 46 iterations and 1.31 seconds (0.45 work units)
Optimal objective 2.36712251e+09
INFO:gurobipy:Optimal objective 2.36712251e+09
INFO:gurobipy:
Crossover log...
INFO:gurobipy:Crossover log...
INFO:gurobipy:
3 DPushes remaining with DInf 0.0000000e+00 1s
INFO:gurobipy: 3 DPushes remaining with DInf 0.0000000e+00 1s
0 DPushes remaining with DInf 0.0000000e+00 1s
INFO:gurobipy: 0 DPushes remaining with DInf 0.0000000e+00 1s
Warning: Markowitz tolerance tightened to 0.25
INFO:gurobipy:Warning: Markowitz tolerance tightened to 0.25
INFO:gurobipy:
3212 PPushes remaining with PInf 0.0000000e+00 1s
INFO:gurobipy: 3212 PPushes remaining with PInf 0.0000000e+00 1s
0 PPushes remaining with PInf 0.0000000e+00 1s
INFO:gurobipy: 0 PPushes remaining with PInf 0.0000000e+00 1s
INFO:gurobipy:
Push phase complete: Pinf 0.0000000e+00, Dinf 1.1673364e-09 1s
INFO:gurobipy: Push phase complete: Pinf 0.0000000e+00, Dinf 1.1673364e-09 1s
INFO:gurobipy:
INFO:gurobipy:
Solved with barrier
INFO:gurobipy:Solved with barrier
Iteration Objective Primal Inf. Dual Inf. Time
INFO:gurobipy:Iteration Objective Primal Inf. Dual Inf. Time
3218 2.3671225e+09 0.000000e+00 0.000000e+00 2s
INFO:gurobipy: 3218 2.3671225e+09 0.000000e+00 0.000000e+00 2s
INFO:gurobipy:
Solved in 3218 iterations and 1.57 seconds (0.84 work units)
INFO:gurobipy:Solved in 3218 iterations and 1.57 seconds (0.84 work units)
Optimal objective 2.367122510e+09
INFO:gurobipy:Optimal objective 2.367122510e+09
INFO:linopy.constants: Optimization successful:
Status: ok
Termination condition: optimal
Solution: 26283 primals, 61324 duals
Objective: 2.37e+09
Solver model: available
Solver message: 2
INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-ext-p-lower, Generator-ext-p-upper were not assigned to the network.
('ok', 'optimal')
network.generators.p_nom_opt #in MW
Generator
onshorewind 19572.434599
solar 8874.293348
OCGT 5229.515916
Name: p_nom_opt, dtype: float64
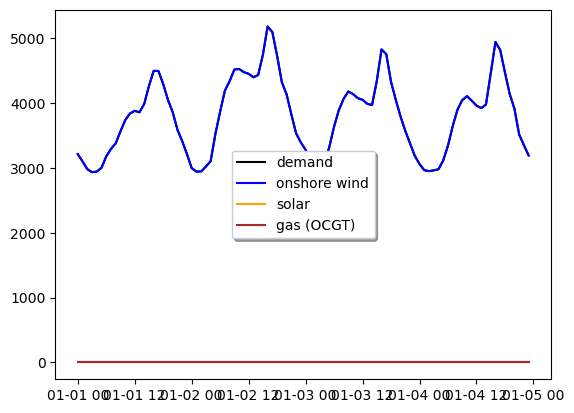
plt.plot(network.loads_t.p['load'][0:96], color='black', label='demand')
plt.plot(network.generators_t.p['onshorewind'][0:96], color='blue', label='onshore wind')
plt.plot(network.generators_t.p['solar'][0:96], color='orange', label='solar')
plt.plot(network.generators_t.p['OCGT'][0:96], color='brown', label='gas (OCGT)')
plt.legend(fancybox=True, shadow=True, loc='best')
<matplotlib.legend.Legend at 0x279f23cb860>
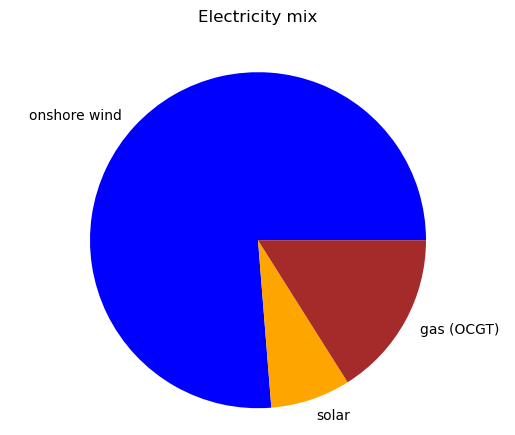
labels = ['onshore wind', 'solar', 'gas (OCGT)' ]
sizes = [network.generators_t.p['onshorewind'].sum(),
network.generators_t.p['solar'].sum(),
network.generators_t.p['OCGT'].sum()]
colors = ['blue', 'orange', 'brown']
plt.pie(sizes,
colors=colors,
labels=labels,
wedgeprops={'linewidth':0})
plt.axis('equal')
plt.title('Electricity mix', y=1.07)
Text(0.5, 1.07, 'Electricity mix')
PROJECT INSTRUCTIONS#
Based on the previous example, you are asked to carry out the following tasks:
A. Choose a different country/region/city/system and calculate the optimal capacities for renewable and non-renewable generators. You can add as many technologies as you want. Remember to provide a reference for the cost assumptions. Plot the dispatch time series for a week in summer and winter. Plot the annual electricity mix. Use the duration curves or the capacity factor to investigate the contribution of different technologies.
B. Investigate how sensitive the optimum capacity mix is to the global CO2 constraint. E.g., plot the generation mix as a function of the CO2 constraint that you impose. Search for the CO2 emissions in your country (today or in 1990) and refer to the emissions allowance to that historical data.
C. Investigate how sensitive your results are to the interannual variability of solar and wind generation. Plot the average capacity and variability obtained for every generator using different weather years.
D. Add some storage technology/ies and investigate how they behave and what their impact is on the optimal system configuration. Discuss what strategies is your system using to balance the renewable generation at different time scales (intraday, seasonal, etc.)
E. Select one target for decarbonization (i.e., one CO2 allowance limit). What is the CO2 price required to achieve that decarbonization level? Search for information on the existing CO2 tax in your country (if any) and discuss your results.
F. Connect your country with, at least, two neighbouring countries. You can connect them using HVAC lines, HVDC links or gas pipelines. Use a linear representation of power flow or gas flow. You can assume that the generation capacities in the neighbouring countries are fixed or optimize the whole system. You can also include fixed interconnection capacities or optimize them with the generators’ capacities. Discuss your results.
G. Connect the electricity sector with, at least, another sector( e.g. heating or transport), and co-optimize all the sectors. Discuss your results.
H. Finally, select one topic that is under discussion in your region. Design and implement some experiment to obtain relevant information regarding that topic. E.g.
What are the consequences if Denmark decides not to install more onshore wind?
Would it be more expensive if France decides to close its nuclear power plants?
What will be the main impacts of the Viking link?
How does gas scarcity impact the optimal system configuration?
Write a short report (maximum length 10 pages) in groups of 4 students including your main findings.
Hints#
HINT 1: You can add a link with the following code
The efficiency will be 1 if you are connecting two countries and different from one if, for example, you are connecting the electricity bus to the heating bus using a heat pump. Setting p_min_pu=-1 makes the link reversible.
network.add("Link",
'country a - country b',
bus0="electricity bus country a",
bus1="electricity bus country b",
p_nom_extendable=True, # capacity is optimised
p_min_pu=-1,
length=600, # length (in km) between country a and country b
capital_cost=400*600) # capital cost * length
WARNING:pypsa.io:The following Link have buses which are not defined:
Index(['country a - country b'], dtype='object')
WARNING:pypsa.io:The following Link have buses which are not defined:
Index(['country a - country b'], dtype='object')
Index(['country a - country b'], dtype='object')
HINT 2: You can check the KKT multiplier associated with the constraint with the following code
print(network.global_constraints.constant) # CO2 limit (constant in the constraint)
print(network.global_constraints.mu) # CO2 price (Lagrance multiplier in the constraint)
GlobalConstraint
co2_limit 1000000.0
Name: constant, dtype: float64
GlobalConstraint
co2_limit -1404.832604
Name: mu, dtype: float64
HINT 3: You can add a H2 store connected to the electricity bus via an electrolyzer and a fuel cell with the following code
#Create a new carrier
network.add("Carrier",
"H2")
#Create a new bus
network.add("Bus",
"H2",
carrier = "H2")
#Connect the store to the bus
network.add("Store",
"H2 Tank",
bus = "H2",
e_nom_extendable = True,
e_cyclic = True,
capital_cost = annuity(25, 0.07)*57000*(1+0.011))
#Add the link "H2 Electrolysis" that transport energy from the electricity bus (bus0) to the H2 bus (bus1)
#with 80% efficiency
network.add("Link",
"H2 Electrolysis",
bus0 = "electricity bus",
bus1 = "H2",
p_nom_extendable = True,
efficiency = 0.8,
capital_cost = annuity(25, 0.07)*600000*(1+0.05))
#Add the link "H2 Fuel Cell" that transports energy from the H2 bus (bus0) to the electricity bus (bus1)
#with 58% efficiency
network.add("Link",
"H2 Fuel Cell",
bus0 = "H2",
bus1 = "electricity bus",
p_nom_extendable = True,
efficiency = 0.58,
capital_cost = annuity(10, 0.07)*1300000*(1+0.05))
HINT 4: You can get inspiration for plotting the flows in the network in the following example
https://pypsa.readthedocs.io/en/latest/examples/flow-plot.html

