Problem 7.3#
Integrated Energy Grids
Problem 7.3
Assume that we have three locations (1,2,3) with an electric bus and a heating bus. The electricity loads are [0, 10, 20] MWh and the heating loads are [30, 20, 10] MWh. The electric buses are connected with transmission lines in a ring and there is a gas power generator at node 1 with an efficiency of 0.3 and a marginal cost of 50 EUR/MWh. At each location the electric and heating buses are connected with heat pumps with a coefficient of performance (COP) of 3; heat can also be supplied to every heat bus with a gas boiler with an efficiency of 0.9 and a marginal cost of 20 EUR/MWh.
(a) Calculate the optimal heat generation by every component and the optical power flowing through the lines.
(b) Repeat (a) assuming that the marginal cost of heat pumps is 10 EUR/MWh.
Note: This problem is based on the PyPSA example LOPF with coupling to heating sector.
Note
If you have not yet set up Python on your computer, you can execute this tutorial in your browser via Google Colab. Click on the rocket in the top right corner and launch “Colab”. If that doesn’t work download the .ipynb file and import it in Google Colab.
Then install the following packages by executing the following command in a Jupyter cell at the top of the notebook.
!pip install numpy pypsa
import matplotlib.pyplot as plt
import pandas as pd
import pypsa
We start by building the network object that will contain the optimization problem
network = pypsa.Network()
Add three buses of AC and heat carrier each
for i in range(3):
network.add("Bus", f"electric bus {i}", v_nom=20.0)
network.add("Bus", f"heat bus {i}", carrier="heat")
network.buses
| v_nom | type | x | y | carrier | unit | location | v_mag_pu_set | v_mag_pu_min | v_mag_pu_max | control | generator | sub_network | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bus | |||||||||||||
| electric bus 0 | 20.0 | 0.0 | 0.0 | AC | 1.0 | 0.0 | inf | PQ | |||||
| heat bus 0 | 1.0 | 0.0 | 0.0 | heat | 1.0 | 0.0 | inf | PQ | |||||
| electric bus 1 | 20.0 | 0.0 | 0.0 | AC | 1.0 | 0.0 | inf | PQ | |||||
| heat bus 1 | 1.0 | 0.0 | 0.0 | heat | 1.0 | 0.0 | inf | PQ | |||||
| electric bus 2 | 20.0 | 0.0 | 0.0 | AC | 1.0 | 0.0 | inf | PQ | |||||
| heat bus 2 | 1.0 | 0.0 | 0.0 | heat | 1.0 | 0.0 | inf | PQ |
Now, we add three transmission lines in a ring
for i in range(3):
network.add(
"Line",
f"line {i}",
bus0=f"electric bus {i}",
bus1=f"electric bus {(i + 1) % 3}",
x=0.1,
s_nom=1000,
)
network.lines
| bus0 | bus1 | type | x | r | g | b | s_nom | s_nom_mod | s_nom_extendable | ... | v_ang_min | v_ang_max | sub_network | x_pu | r_pu | g_pu | b_pu | x_pu_eff | r_pu_eff | s_nom_opt | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Line | |||||||||||||||||||||
| line 0 | electric bus 0 | electric bus 1 | 0.1 | 0.0 | 0.0 | 0.0 | 1000.0 | 0.0 | False | ... | -inf | inf | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| line 1 | electric bus 1 | electric bus 2 | 0.1 | 0.0 | 0.0 | 0.0 | 1000.0 | 0.0 | False | ... | -inf | inf | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| line 2 | electric bus 2 | electric bus 0 | 0.1 | 0.0 | 0.0 | 0.0 | 1000.0 | 0.0 | False | ... | -inf | inf | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
3 rows × 31 columns
We connect every electricity bus to its corresponding heat bus using a heat pump with Coefficient of Performance (COP) 3
for i in range(3):
network.add(
"Link",
f"heat pump {i}",
bus0=f"electric bus {i}",
bus1=f"heat bus {i}",
p_nom=100,
efficiency=3.0,
)
network.links
| bus0 | bus1 | type | carrier | efficiency | active | build_year | lifetime | p_nom | p_nom_mod | ... | shut_down_cost | min_up_time | min_down_time | up_time_before | down_time_before | ramp_limit_up | ramp_limit_down | ramp_limit_start_up | ramp_limit_shut_down | p_nom_opt | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Link | |||||||||||||||||||||
| heat pump 0 | electric bus 0 | heat bus 0 | 3.0 | True | 0 | inf | 100.0 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| heat pump 1 | electric bus 1 | heat bus 1 | 3.0 | True | 0 | inf | 100.0 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| heat pump 2 | electric bus 2 | heat bus 2 | 3.0 | True | 0 | inf | 100.0 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 |
3 rows × 34 columns
We add a gas generator at electric bus 0 and a boiler at all heat buses
network.add(
"Generator",
"gas generator",
bus="electric bus 0",
p_nom=100,
marginal_cost=50,
efficiency=0.3,
)
for i in range(3):
network.add(
"Generator",
f"boiler {i}",
bus=f"heat bus {i}",
p_nom=1000,
efficiency=0.9,
marginal_cost=20.0,
carrier="gas",
)
network.generators
| bus | control | type | p_nom | p_nom_mod | p_nom_extendable | p_nom_min | p_nom_max | p_min_pu | p_max_pu | ... | min_up_time | min_down_time | up_time_before | down_time_before | ramp_limit_up | ramp_limit_down | ramp_limit_start_up | ramp_limit_shut_down | weight | p_nom_opt | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Generator | |||||||||||||||||||||
| gas generator | electric bus 0 | PQ | 100.0 | 0.0 | False | 0.0 | inf | 0.0 | 1.0 | ... | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 1.0 | 0.0 | |
| boiler 0 | heat bus 0 | PQ | 1000.0 | 0.0 | False | 0.0 | inf | 0.0 | 1.0 | ... | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 1.0 | 0.0 | |
| boiler 1 | heat bus 1 | PQ | 1000.0 | 0.0 | False | 0.0 | inf | 0.0 | 1.0 | ... | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 1.0 | 0.0 | |
| boiler 2 | heat bus 2 | PQ | 1000.0 | 0.0 | False | 0.0 | inf | 0.0 | 1.0 | ... | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 1.0 | 0.0 |
4 rows × 37 columns
Add electric loads and heat loads.
for i in range(3):
network.add(
"Load",
f"electric load {i}",
bus=f"electric bus {i}",
p_set=i * 10,
)
for i in range(3):
network.add(
"Load",
f"heat load {i}",
bus=f"heat bus {i}",
p_set=(3 - i) * 10,
)
network.loads
| bus | carrier | type | p_set | q_set | sign | active | |
|---|---|---|---|---|---|---|---|
| Load | |||||||
| electric load 0 | electric bus 0 | 0.0 | 0.0 | -1.0 | True | ||
| electric load 1 | electric bus 1 | 10.0 | 0.0 | -1.0 | True | ||
| electric load 2 | electric bus 2 | 20.0 | 0.0 | -1.0 | True | ||
| heat load 0 | heat bus 0 | 30.0 | 0.0 | -1.0 | True | ||
| heat load 1 | heat bus 1 | 20.0 | 0.0 | -1.0 | True | ||
| heat load 2 | heat bus 2 | 10.0 | 0.0 | -1.0 | True |
network.optimize()
WARNING:pypsa.consistency:The following generators have carriers which are not defined:
Index(['boiler 0', 'boiler 1', 'boiler 2'], dtype='object', name='Generator')
WARNING:pypsa.consistency:The following lines have carriers which are not defined:
Index(['line 0', 'line 1', 'line 2'], dtype='object', name='Line')
WARNING:pypsa.consistency:The following lines have zero r, which could break the linear load flow:
Index(['line 0', 'line 1', 'line 2'], dtype='object', name='Line')
WARNING:pypsa.consistency:The following links have carriers which are not defined:
Index(['heat pump 0', 'heat pump 1', 'heat pump 2'], dtype='object', name='Link')
WARNING:pypsa.consistency:The following buses have carriers which are not defined:
Index(['electric bus 0', 'heat bus 0', 'electric bus 1', 'heat bus 1',
'electric bus 2', 'heat bus 2'],
dtype='object', name='Bus')
INFO:linopy.model: Solve problem using Highs solver
INFO:linopy.io: Writing time: 0.03s
INFO:linopy.constants: Optimization successful:
Status: ok
Termination condition: optimal
Solution: 10 primals, 27 duals
Objective: 2.50e+03
Solver model: available
Solver message: Optimal
INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Line-fix-s-lower, Line-fix-s-upper, Link-fix-p-lower, Link-fix-p-upper, Kirchhoff-Voltage-Law were not assigned to the network.
Running HiGHS 1.10.0 (git hash: fd86653): Copyright (c) 2025 HiGHS under MIT licence terms
LP linopy-problem-pyd_fs6m has 27 rows; 10 cols; 39 nonzeros
Coefficient ranges:
Matrix [1e+00, 2e+01]
Cost [2e+01, 5e+01]
Bound [0e+00, 0e+00]
RHS [1e+01, 1e+03]
Presolving model
4 rows, 7 cols, 13 nonzeros 0s
3 rows, 6 cols, 11 nonzeros 0s
2 rows, 5 cols, 7 nonzeros 0s
1 rows, 4 cols, 4 nonzeros 0s
0 rows, 0 cols, 0 nonzeros 0s
Presolve : Reductions: rows 0(-27); columns 0(-10); elements 0(-39) - Reduced to empty
Solving the original LP from the solution after postsolve
Model name : linopy-problem-pyd_fs6m
Model status : Optimal
Objective value : 2.5000000000e+03
Relative P-D gap : 1.8189894035e-16
HiGHS run time : 0.00
Writing the solution to /tmp/linopy-solve-lelceuqq.sol
('ok', 'optimal')
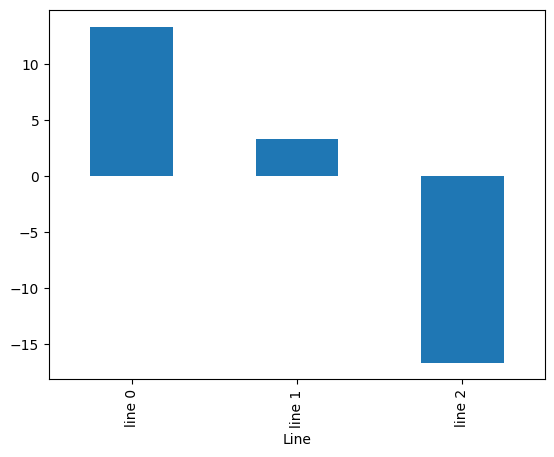
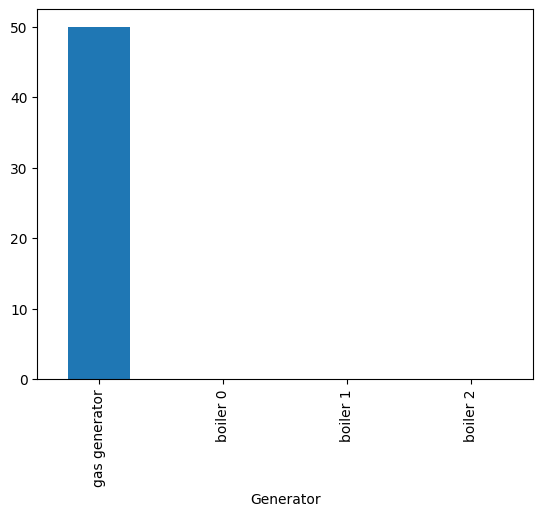
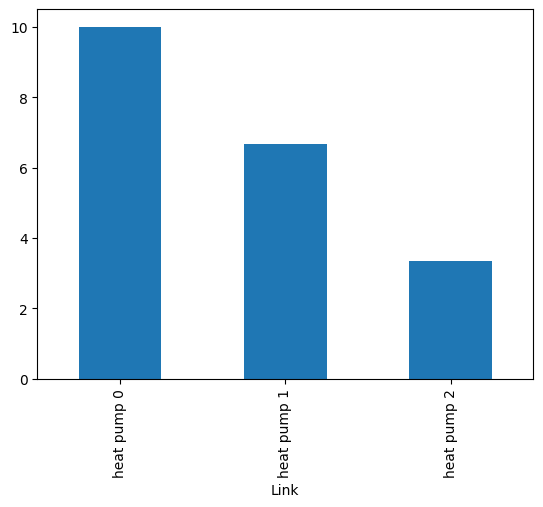
We can calculate and plot the energy produced by every boiler, heat pumps and trasmitted through the lines
demands = network.loads_t.p.loc["now"]
generators = network.generators_t.p.loc["now"]
links = network.links_t.p0.loc["now"]
lines = network.lines_t.p0.loc["now"]
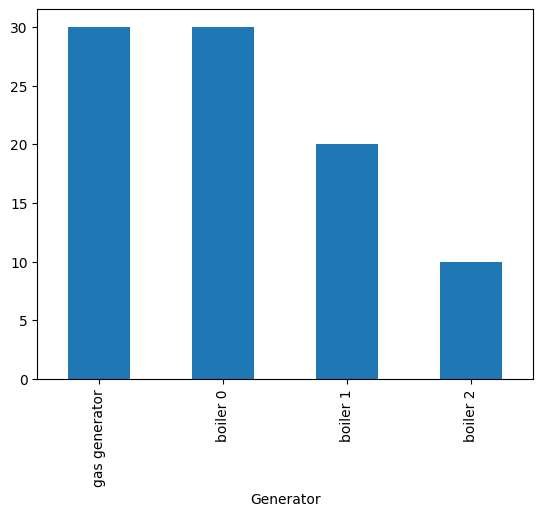
generators.plot.bar()
<Axes: xlabel='Generator'>
links.plot.bar()
<Axes: xlabel='Link'>
lines.plot.bar()
<Axes: xlabel='Line'>
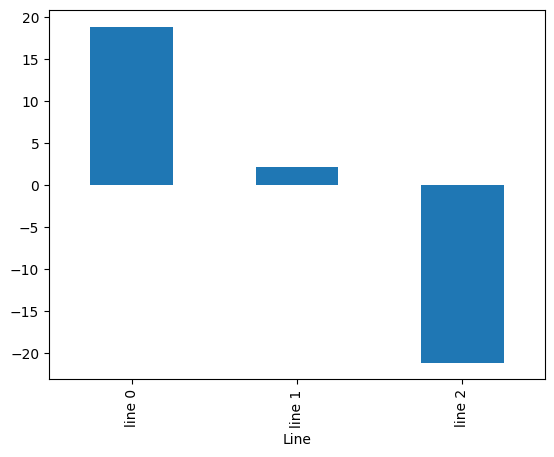
(b) Repeat (a) assuming that the marginal cost of heat pumps is 10 EUR/MWh.
We update the marginal cost of heat pumps and redo the optimization
network.links.marginal_cost = 10
network.optimize()
demands = network.loads_t.p.loc["now"]
generators = network.generators_t.p.loc["now"]
links = network.links_t.p0.loc["now"]
lines = network.lines_t.p0.loc["now"]
WARNING:pypsa.consistency:The following sub_networks have carriers which are not defined:
Index(['0'], dtype='object', name='SubNetwork')
WARNING:pypsa.consistency:The following generators have carriers which are not defined:
Index(['boiler 0', 'boiler 1', 'boiler 2'], dtype='object', name='Generator')
WARNING:pypsa.consistency:The following lines have carriers which are not defined:
Index(['line 0', 'line 1', 'line 2'], dtype='object', name='Line')
WARNING:pypsa.consistency:The following lines have zero r, which could break the linear load flow:
Index(['line 0', 'line 1', 'line 2'], dtype='object', name='Line')
WARNING:pypsa.consistency:The following links have carriers which are not defined:
Index(['heat pump 0', 'heat pump 1', 'heat pump 2'], dtype='object', name='Link')
WARNING:pypsa.consistency:The following buses have carriers which are not defined:
Index(['electric bus 0', 'heat bus 0', 'electric bus 1', 'heat bus 1',
'electric bus 2', 'heat bus 2'],
dtype='object', name='Bus')
INFO:linopy.model: Solve problem using Highs solver
INFO:linopy.io: Writing time: 0.03s
INFO:linopy.constants: Optimization successful:
Status: ok
Termination condition: optimal
Solution: 10 primals, 27 duals
Objective: 2.70e+03
Solver model: available
Solver message: Optimal
INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Line-fix-s-lower, Line-fix-s-upper, Link-fix-p-lower, Link-fix-p-upper, Kirchhoff-Voltage-Law were not assigned to the network.
Running HiGHS 1.10.0 (git hash: fd86653): Copyright (c) 2025 HiGHS under MIT licence terms
LP linopy-problem-wydzc3fr has 27 rows; 10 cols; 39 nonzeros
Coefficient ranges:
Matrix [1e+00, 2e+01]
Cost [1e+01, 5e+01]
Bound [0e+00, 0e+00]
RHS [1e+01, 1e+03]
Presolving model
4 rows, 7 cols, 13 nonzeros 0s
3 rows, 6 cols, 11 nonzeros 0s
2 rows, 5 cols, 7 nonzeros 0s
1 rows, 4 cols, 4 nonzeros 0s
0 rows, 0 cols, 0 nonzeros 0s
Presolve : Reductions: rows 0(-27); columns 0(-10); elements 0(-39) - Reduced to empty
Solving the original LP from the solution after postsolve
Model name : linopy-problem-wydzc3fr
Model status : Optimal
Objective value : 2.7000000000e+03
Relative P-D gap : 0.0000000000e+00
HiGHS run time : 0.00
Writing the solution to /tmp/linopy-solve-zcaedls5.sol
generators.plot.bar()
<Axes: xlabel='Generator'>
links.plot.bar()
<Axes: xlabel='Link'>
lines.plot.bar()
<Axes: xlabel='Line'>