Problem 6.1#
Integrated Energy Grids
Problem 6.1
Consider the simplified network plotted in Fig. 1, which represents Denmark and its neighbouring countries. Assume that the nodes are connected using transmission methane gas pipelines.
(a) Calculate the capacity of every pipeline (in MW) assuming that they operate at a pressure \(P\)=50 bar, the average gas flow velocity is \(u\) = 15 m/s, the diameter of the pipes is \(D\) = 600mm and the energy content of methane is 50 GJ/tonne. To calculate the speed of sound in gas \(c\), assume the universal gas constant \(R\)=8.314 J/molK, the molar mass of methane \(M\)=16 g/mol, compression factor \(Z\)=1.31, and temperature \(T\)=25\(^{\circ}\)C.
Note
If you have not yet set up Python on your computer, you can execute this tutorial in your browser via Google Colab. Click on the rocket in the top right corner and launch “Colab”. If that doesn’t work download the .ipynb file and import it in Google Colab.
Then install the following packages by executing the following command in a Jupyter cell at the top of the notebook.
!pip install numpy pypsa
import numpy as np
import pypsa
The cross-sectional area \(A\) and the speed of sound in gas \(c\) can be calculated as
D = 0.6 # m
u = 15 # m/s
P = 50*100000 #Pa
Z = 1.31
R = 8.314 # J/molK
M = 0.016 # Kg/mol
T = 273+25 # K
e = 50 # GJ/tonne or MJ/kg
A = np.pi*(D/2)**2
c=np.sqrt(Z*R*T/M)
c
np.float64(450.3900615022494)
The density can be calculated as
rho = P / c**2
rho
np.float64(24.648608512719843)
The capacity of every pipeline can be calculated as \(Q = \rho A u e\)
capacity = rho*A*u*e
capacity
np.float64(5226.922401172076)
So, we obtain that the capacity is aproximately 5.2 GW
(b) Assuming steady-state conditions, use link elements in PyPSA to build a network like the one shown in Fig. 1. Assume that, in the first time step, in every node, there is a demand for 5 GWh of methane. In the Norway node there is a gas generator with a marginal cost of 20 EUR/MWh\(_{th}\). Calculate the optimal gas flows through the network and plot them.
We start by creating the network object and adding the buses or nodes
network = pypsa.Network()
nodes = ["DE", "DK1", "DK2", "NO", "SE"]
pos = [[0, 0],[0, 1],[1, 1],[0, 2],[1, 2]] # We add the nodes' position only to make the plot later look pretty
for i,node in enumerate(nodes):
network.add("Bus",
"bus {}".format(node),
x=pos[i][0],
y=pos[i][1])
network.buses
| v_nom | type | x | y | carrier | unit | location | v_mag_pu_set | v_mag_pu_min | v_mag_pu_max | control | generator | sub_network | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bus | |||||||||||||
| bus DE | 1.0 | 0.0 | 0.0 | AC | 1.0 | 0.0 | inf | PQ | |||||
| bus DK1 | 1.0 | 0.0 | 1.0 | AC | 1.0 | 0.0 | inf | PQ | |||||
| bus DK2 | 1.0 | 1.0 | 1.0 | AC | 1.0 | 0.0 | inf | PQ | |||||
| bus NO | 1.0 | 0.0 | 2.0 | AC | 1.0 | 0.0 | inf | PQ | |||||
| bus SE | 1.0 | 1.0 | 2.0 | AC | 1.0 | 0.0 | inf | PQ |
We add the links representing the gas pipelines
network.add("Link","pipeline DE-DK1", bus0 = "bus DE", bus1 = "bus DK1", p_nom = capacity, p_min_pu=-1) #p_min_pu makes the pipeline reversible
network.add("Link","pipeline DK1-DK2", bus0 = "bus DK1", bus1 = "bus DK2", p_nom = capacity, p_min_pu=-1)
network.add("Link","pipeline DK1-NO", bus0 = "bus DK1", bus1 = "bus NO", p_nom = capacity, p_min_pu=-1)
network.add("Link","pipeline DK1-SE", bus0 = "bus DK1", bus1 = "bus SE", p_nom = capacity, p_min_pu=-1)
network.add("Link","pipeline DK2-SE", bus0 = "bus DK2", bus1 = "bus SE", p_nom = capacity, p_min_pu=-1)
network.links
| bus0 | bus1 | type | carrier | efficiency | active | build_year | lifetime | p_nom | p_nom_mod | ... | shut_down_cost | min_up_time | min_down_time | up_time_before | down_time_before | ramp_limit_up | ramp_limit_down | ramp_limit_start_up | ramp_limit_shut_down | p_nom_opt | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Link | |||||||||||||||||||||
| pipeline DE-DK1 | bus DE | bus DK1 | 1.0 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK1-DK2 | bus DK1 | bus DK2 | 1.0 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK1-NO | bus DK1 | bus NO | 1.0 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK1-SE | bus DK1 | bus SE | 1.0 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK2-SE | bus DK2 | bus SE | 1.0 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 |
5 rows × 34 columns
nodes
['DE', 'DK1', 'DK2', 'NO', 'SE']
We add the loads and generator
for node in nodes:
network.add("Load",
"gas demand {}".format(node),
bus="bus {}".format(node),
p_set=1000) #demand 1GWh = 1,000 MWh
network.loads
| bus | carrier | type | p_set | q_set | sign | active | |
|---|---|---|---|---|---|---|---|
| Load | |||||||
| gas demand DE | bus DE | 1000.0 | 0.0 | -1.0 | True | ||
| gas demand DK1 | bus DK1 | 1000.0 | 0.0 | -1.0 | True | ||
| gas demand DK2 | bus DK2 | 1000.0 | 0.0 | -1.0 | True | ||
| gas demand NO | bus NO | 1000.0 | 0.0 | -1.0 | True | ||
| gas demand SE | bus SE | 1000.0 | 0.0 | -1.0 | True |
network.add("Generator",
"gas",
bus="bus NO",
p_nom=10000, #not relevant, just set it so that it is not limiting
marginal_cost=20) #EUR/MWh_th
network.generators
| bus | control | type | p_nom | p_nom_mod | p_nom_extendable | p_nom_min | p_nom_max | p_min_pu | p_max_pu | ... | min_up_time | min_down_time | up_time_before | down_time_before | ramp_limit_up | ramp_limit_down | ramp_limit_start_up | ramp_limit_shut_down | weight | p_nom_opt | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Generator | |||||||||||||||||||||
| gas | bus NO | PQ | 10000.0 | 0.0 | False | 0.0 | inf | 0.0 | 1.0 | ... | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 1.0 | 0.0 |
1 rows × 37 columns
network.optimize()
WARNING:pypsa.consistency:The following buses have carriers which are not defined:
Index(['bus DE', 'bus DK1', 'bus DK2', 'bus NO', 'bus SE'], dtype='object', name='Bus')
WARNING:pypsa.consistency:The following links have carriers which are not defined:
Index(['pipeline DE-DK1', 'pipeline DK1-DK2', 'pipeline DK1-NO',
'pipeline DK1-SE', 'pipeline DK2-SE'],
dtype='object', name='Link')
INFO:linopy.model: Solve problem using Highs solver
INFO:linopy.io: Writing time: 0.02s
INFO:linopy.constants: Optimization successful:
Status: ok
Termination condition: optimal
Solution: 6 primals, 17 duals
Objective: 1.00e+05
Solver model: available
Solver message: Optimal
INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Link-fix-p-lower, Link-fix-p-upper were not assigned to the network.
Running HiGHS 1.10.0 (git hash: fd86653): Copyright (c) 2025 HiGHS under MIT licence terms
LP linopy-problem-gfnvd1i0 has 17 rows; 6 cols; 23 nonzeros
Coefficient ranges:
Matrix [1e+00, 1e+00]
Cost [2e+01, 2e+01]
Bound [0e+00, 0e+00]
RHS [1e+03, 1e+04]
Presolving model
0 rows, 0 cols, 0 nonzeros 0s
0 rows, 0 cols, 0 nonzeros 0s
Presolve : Reductions: rows 0(-17); columns 0(-6); elements 0(-23) - Reduced to empty
Solving the original LP from the solution after postsolve
Model name : linopy-problem-gfnvd1i0
Model status : Optimal
Objective value : 1.0000000000e+05
Relative P-D gap : 0.0000000000e+00
HiGHS run time : 0.00
Writing the solution to /tmp/linopy-solve-63u8ykhn.sol
('ok', 'optimal')
network.generators_t.p
| Generator | gas |
|---|---|
| snapshot | |
| now | 5000.0 |
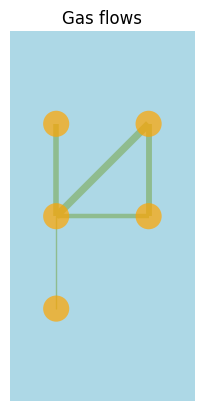
gas_flows=network.links_t.p0.loc['now']/1000 #MWh->GWh
gas_flows
Link
pipeline DE-DK1 -1.000000
pipeline DK1-DK2 -3.226922
pipeline DK1-NO -4.000000
pipeline DK1-SE 5.226922
pipeline DK2-SE -4.226922
Name: now, dtype: float64
network.plot(
margin=0.5,
bus_colors="orange",
bus_alpha=0.7,
color_geomap=True,
link_widths=abs(gas_flows),
title="Gas flows",
);
/tmp/ipykernel_2649/3962336250.py:1: DeprecatedWarning: plot is deprecated. Use `n.plot.map()` as a drop-in replacement instead.
network.plot(
/opt/hostedtoolcache/Python/3.11.12/x64/lib/python3.11/site-packages/pypsa/plot/accessor.py:34: DeprecationWarning: `color_geomap` is deprecated as an argument to `plot`; use `geomap_colors` instead.
return plot(self.n, *args, **kwargs)
/opt/hostedtoolcache/Python/3.11.12/x64/lib/python3.11/site-packages/cartopy/io/__init__.py:241: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/50m_physical/ne_50m_land.zip
warnings.warn(f'Downloading: {url}', DownloadWarning)
/opt/hostedtoolcache/Python/3.11.12/x64/lib/python3.11/site-packages/cartopy/io/__init__.py:241: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/50m_physical/ne_50m_ocean.zip
warnings.warn(f'Downloading: {url}', DownloadWarning)
/opt/hostedtoolcache/Python/3.11.12/x64/lib/python3.11/site-packages/cartopy/io/__init__.py:241: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/50m_cultural/ne_50m_admin_0_boundary_lines_land.zip
warnings.warn(f'Downloading: {url}', DownloadWarning)
/opt/hostedtoolcache/Python/3.11.12/x64/lib/python3.11/site-packages/cartopy/io/__init__.py:241: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/50m_physical/ne_50m_coastline.zip
warnings.warn(f'Downloading: {url}', DownloadWarning)
(c) Assume the following lengths for the links: DK1-DK2=200 km, DK1-DE=600 km, DK1-NO= 500 km, DK1-SE=600 km, DK2-SE=100 km. If we consider that the losses due to energy consumption of the compressors’ to maintain the pressure can be estimated at 2% of the energy flow per 1000 km. Adapt the link elements in PyPSA to include an efficiency that takes compressors’ energy demand into account. calculate the optimal gas flows through the network and plot them.
losses_per_1000km = 0.02 #%
Since we want to represent losses by imposing a certain efficiency in the links, we can not anymore define them as reversible by making p_min_pu=-1 and we need to duplicate and reverse the links.
network.add("Link","pipeline DE-DK1", bus0 = "bus DE", bus1 = "bus DK1", efficiency = 1-600/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline DK1-DK2", bus0 = "bus DK1", bus1 = "bus DK2", efficiency = 1-200/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline DK1-NO", bus0 = "bus DK1", bus1 = "bus NO", efficiency = 1-500/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline DK1-SE", bus0 = "bus DK1", bus1 = "bus SE", efficiency = 1-600/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline DK2-SE", bus0 = "bus DK2", bus1 = "bus SE", efficiency = 1-100/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline DK1-DE", bus1 = "bus DE", bus0 = "bus DK1", efficiency = 1-600/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline DK2-DK1", bus1 = "bus DK1", bus0 = "bus DK2", efficiency = 1-200/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline NO-DK1", bus1 = "bus DK1", bus0 = "bus NO", efficiency = 1-500/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline SE-DK1", bus1 = "bus DK1", bus0 = "bus SE", efficiency = 1-600/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline SE-DK2", bus1 = "bus DK2", bus0 = "bus SE", efficiency = 1-100/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.links
| bus0 | bus1 | type | carrier | efficiency | active | build_year | lifetime | p_nom | p_nom_mod | ... | shut_down_cost | min_up_time | min_down_time | up_time_before | down_time_before | ramp_limit_up | ramp_limit_down | ramp_limit_start_up | ramp_limit_shut_down | p_nom_opt | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Link | |||||||||||||||||||||
| pipeline DE-DK1 | bus DE | bus DK1 | 0.988 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK1-DK2 | bus DK1 | bus DK2 | 0.996 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK1-NO | bus DK1 | bus NO | 0.990 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK1-SE | bus DK1 | bus SE | 0.988 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK2-SE | bus DK2 | bus SE | 0.998 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK1-DE | bus DK1 | bus DE | 0.988 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK2-DK1 | bus DK2 | bus DK1 | 0.996 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline NO-DK1 | bus NO | bus DK1 | 0.990 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline SE-DK1 | bus SE | bus DK1 | 0.988 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline SE-DK2 | bus SE | bus DK2 | 0.998 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 |
10 rows × 34 columns
network.optimize()
WARNING:pypsa.consistency:The following buses have carriers which are not defined:
Index(['bus DE', 'bus DK1', 'bus DK2', 'bus NO', 'bus SE'], dtype='object', name='Bus')
WARNING:pypsa.consistency:The following links have carriers which are not defined:
Index(['pipeline DE-DK1', 'pipeline DK1-DK2', 'pipeline DK1-NO',
'pipeline DK1-SE', 'pipeline DK2-SE', 'pipeline DK1-DE',
'pipeline DK2-DK1', 'pipeline NO-DK1', 'pipeline SE-DK1',
'pipeline SE-DK2'],
dtype='object', name='Link')
INFO:linopy.model: Solve problem using Highs solver
INFO:linopy.io: Writing time: 0.02s
INFO:linopy.constants: Optimization successful:
Status: ok
Termination condition: optimal
Solution: 11 primals, 27 duals
Objective: 1.01e+05
Solver model: available
Solver message: Optimal
INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Link-fix-p-lower, Link-fix-p-upper were not assigned to the network.
Running HiGHS 1.10.0 (git hash: fd86653): Copyright (c) 2025 HiGHS under MIT licence terms
LP linopy-problem-n2mt5doe has 27 rows; 11 cols; 43 nonzeros
Coefficient ranges:
Matrix [1e+00, 1e+00]
Cost [2e+01, 2e+01]
Bound [0e+00, 0e+00]
RHS [1e+03, 1e+04]
Presolving model
4 rows, 10 cols, 18 nonzeros 0s
Dependent equations search running on 4 equations with time limit of 1000.00s
Dependent equations search removed 0 rows and 0 nonzeros in 0.00s (limit = 1000.00s)
4 rows, 10 cols, 18 nonzeros 0s
Presolve : Reductions: rows 4(-23); columns 10(-1); elements 18(-25)
Solving the presolved LP
Using EKK dual simplex solver - serial
Iteration Objective Infeasibilities num(sum)
0 5.0487388926e-04 Pr: 4(5012.15) 0s
6 1.0125636230e+05 Pr: 0(0) 0s
Solving the original LP from the solution after postsolve
Model name : linopy-problem-n2mt5doe
Model status : Optimal
Simplex iterations: 6
Objective value : 1.0125636230e+05
Relative P-D gap : 0.0000000000e+00
HiGHS run time : 0.00
Writing the solution to /tmp/linopy-solve-94ywqy4f.sol
('ok', 'optimal')
network.generators_t.p
| Generator | gas |
|---|---|
| snapshot | |
| now | 5062.818115 |
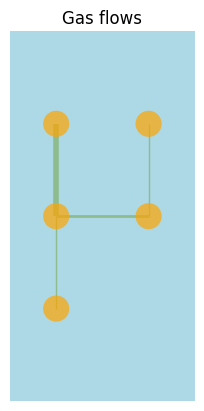
gas_flows=network.links_t.p0.loc['now']/1000 #MWh->GWh
gas_flows
Link
pipeline DE-DK1 -0.000000
pipeline DK1-DK2 2.010044
pipeline DK1-NO -0.000000
pipeline DK1-SE -0.000000
pipeline DK2-SE 1.002004
pipeline DK1-DE 1.012146
pipeline DK2-DK1 -0.000000
pipeline NO-DK1 4.062818
pipeline SE-DK1 -0.000000
pipeline SE-DK2 -0.000000
Name: now, dtype: float64
network.plot(
margin=0.5,
bus_colors="orange",
bus_alpha=0.7,
color_geomap=True,
link_widths=gas_flows,
title="Gas flows",
);
/tmp/ipykernel_2649/526667820.py:1: DeprecatedWarning: plot is deprecated. Use `n.plot.map()` as a drop-in replacement instead.
network.plot(
/opt/hostedtoolcache/Python/3.11.12/x64/lib/python3.11/site-packages/pypsa/plot/accessor.py:34: DeprecationWarning: `color_geomap` is deprecated as an argument to `plot`; use `geomap_colors` instead.
return plot(self.n, *args, **kwargs)
(d) Assuming the following demands in GWh for three consecutive time steps DE=[0,0,3], DK1=[1,2,1], DK2=[1,1,1], NO=[1,1,1], SE=[0,1,0]. Calculate the optimal flows in every time step and the total system costs.
We create the network again but this time with 3 time steps.
network=pypsa.Network(snapshots=range(3))
for i,node in enumerate(nodes):
network.add("Bus",
"bus {}".format(node),
x=pos[i][0],
y=pos[i][1])
network.add("Generator",
"gas",
bus="bus NO",
p_nom=100000, #not relevant, just set so that it is not limiting
marginal_cost=20) #EUR/MWh_th
network.add("Link","pipeline DE-DK1", bus0 = "bus DE", bus1 = "bus DK1", efficiency = 1-600/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline DK1-DK2", bus0 = "bus DK1", bus1 = "bus DK2", efficiency = 1-200/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline DK1-NO", bus0 = "bus DK1", bus1 = "bus NO", efficiency = 1-500/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline DK1-SE", bus0 = "bus DK1", bus1 = "bus SE", efficiency = 1-600/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline DK2-SE", bus0 = "bus DK2", bus1 = "bus SE", efficiency = 1-100/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline DK1-DE", bus1 = "bus DE", bus0 = "bus DK1", efficiency = 1-600/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline DK2-DK1", bus1 = "bus DK1", bus0 = "bus DK2", efficiency = 1-200/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline NO-DK1", bus1 = "bus DK1", bus0 = "bus NO", efficiency = 1-500/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline SE-DK1", bus1 = "bus DK1", bus0 = "bus SE", efficiency = 1-600/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.add("Link","pipeline SE-DK2", bus1 = "bus DK2", bus0 = "bus SE", efficiency = 1-100/1000*losses_per_1000km, overwrite=True, p_nom = capacity)
network.links
| bus0 | bus1 | type | carrier | efficiency | active | build_year | lifetime | p_nom | p_nom_mod | ... | shut_down_cost | min_up_time | min_down_time | up_time_before | down_time_before | ramp_limit_up | ramp_limit_down | ramp_limit_start_up | ramp_limit_shut_down | p_nom_opt | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Link | |||||||||||||||||||||
| pipeline DE-DK1 | bus DE | bus DK1 | 0.988 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK1-DK2 | bus DK1 | bus DK2 | 0.996 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK1-NO | bus DK1 | bus NO | 0.990 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK1-SE | bus DK1 | bus SE | 0.988 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK2-SE | bus DK2 | bus SE | 0.998 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK1-DE | bus DK1 | bus DE | 0.988 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline DK2-DK1 | bus DK2 | bus DK1 | 0.996 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline NO-DK1 | bus NO | bus DK1 | 0.990 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline SE-DK1 | bus SE | bus DK1 | 0.988 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 | ||
| pipeline SE-DK2 | bus SE | bus DK2 | 0.998 | True | 0 | inf | 5226.922401 | 0.0 | ... | 0.0 | 0 | 0 | 1 | 0 | NaN | NaN | 1.0 | 1.0 | 0.0 |
10 rows × 34 columns
We add the load in every node.
loads=[[0,0,3000],
[1000,2000,1000],
[1000,1000,1000],
[1000,1000,1000],
[0,1000,0]]
for i, node in enumerate(nodes):
network.add("Load",
"gas demand {}".format(node),
bus="bus {}".format(node),
p_set=loads[i],
overwrite=True)
network.loads_t
{'p_set': Load gas demand DE gas demand DK1 gas demand DK2 gas demand NO \
snapshot
0 0.0 1000.0 1000.0 1000.0
1 0.0 2000.0 1000.0 1000.0
2 3000.0 1000.0 1000.0 1000.0
Load gas demand SE
snapshot
0 0.0
1 1000.0
2 0.0 ,
'q_set': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'p': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'q': Empty DataFrame
Columns: []
Index: [0, 1, 2]}
network.optimize()
WARNING:pypsa.consistency:The following buses have carriers which are not defined:
Index(['bus DE', 'bus DK1', 'bus DK2', 'bus NO', 'bus SE'], dtype='object', name='Bus')
WARNING:pypsa.consistency:The following links have carriers which are not defined:
Index(['pipeline DE-DK1', 'pipeline DK1-DK2', 'pipeline DK1-NO',
'pipeline DK1-SE', 'pipeline DK2-SE', 'pipeline DK1-DE',
'pipeline DK2-DK1', 'pipeline NO-DK1', 'pipeline SE-DK1',
'pipeline SE-DK2'],
dtype='object', name='Link')
INFO:linopy.model: Solve problem using Highs solver
INFO:linopy.io: Writing time: 0.02s
INFO:linopy.constants: Optimization successful:
Status: ok
Termination condition: optimal
Solution: 33 primals, 81 duals
Objective: 2.83e+05
Solver model: available
Solver message: Optimal
INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Link-fix-p-lower, Link-fix-p-upper were not assigned to the network.
Running HiGHS 1.10.0 (git hash: fd86653): Copyright (c) 2025 HiGHS under MIT licence terms
LP linopy-problem-lu36uurr has 81 rows; 33 cols; 129 nonzeros
Coefficient ranges:
Matrix [1e+00, 1e+00]
Cost [2e+01, 2e+01]
Bound [0e+00, 0e+00]
RHS [1e+03, 1e+05]
Presolving model
12 rows, 30 cols, 54 nonzeros 0s
Dependent equations search running on 12 equations with time limit of 1000.00s
Dependent equations search removed 0 rows and 0 nonzeros in 0.00s (limit = 1000.00s)
12 rows, 30 cols, 54 nonzeros 0s
Presolve : Reductions: rows 12(-69); columns 30(-3); elements 54(-75)
Solving the presolved LP
Using EKK dual simplex solver - serial
Iteration Objective Infeasibilities num(sum)
0 1.1758012135e-03 Pr: 10(14036.4) 0s
18 2.8332350627e+05 Pr: 0(0) 0s
Solving the original LP from the solution after postsolve
Model name : linopy-problem-lu36uurr
Model status : Optimal
Simplex iterations: 18
Objective value : 2.8332350627e+05
Relative P-D gap : 2.0544592886e-16
HiGHS run time : 0.00
Writing the solution to /tmp/linopy-solve-07io50nd.sol
('ok', 'optimal')
We can see the gas flows in every pipeline using
network.links_t.p0
| Link | pipeline DE-DK1 | pipeline DK1-DK2 | pipeline DK1-NO | pipeline DK1-SE | pipeline DK2-SE | pipeline DK1-DE | pipeline DK2-DK1 | pipeline NO-DK1 | pipeline SE-DK1 | pipeline SE-DK2 |
|---|---|---|---|---|---|---|---|---|---|---|
| snapshot | ||||||||||
| 0 | -0.0 | 1004.016064 | -0.0 | -0.0 | -0.000000 | -0.000000 | -0.0 | 2024.258651 | -0.0 | -0.0 |
| 1 | -0.0 | 2010.044185 | -0.0 | -0.0 | 1002.004008 | -0.000000 | -0.0 | 4050.549682 | -0.0 | -0.0 |
| 2 | -0.0 | 1004.016064 | -0.0 | -0.0 | -0.000000 | 3036.437247 | -0.0 | 5091.366981 | -0.0 | -0.0 |
And the total system cost is
network.objective
283323.50626732665
(e) Modify the demand for the German node to be DE=[0,0,6] GWh and keep the other node as in the previous section. Calculate the optimal flows in every time step and the total system costs.
network.add("Load",
"gas demand DE",
bus="bus DE",
p_set=[0,0,6000],
overwrite=True)
network.optimize()
WARNING:pypsa.consistency:The following buses have carriers which are not defined:
Index(['bus DE', 'bus DK1', 'bus DK2', 'bus NO', 'bus SE'], dtype='object', name='Bus')
WARNING:pypsa.consistency:The following links have carriers which are not defined:
Index(['pipeline DE-DK1', 'pipeline DK1-DK2', 'pipeline DK1-NO',
'pipeline DK1-SE', 'pipeline DK2-SE', 'pipeline DK1-DE',
'pipeline DK2-DK1', 'pipeline NO-DK1', 'pipeline SE-DK1',
'pipeline SE-DK2'],
dtype='object', name='Link')
INFO:linopy.model: Solve problem using Highs solver
INFO:linopy.io: Writing time: 0.02s
WARNING:linopy.constants:Optimization potentially failed:
Status: warning
Termination condition: infeasible
Solution: 0 primals, 0 duals
Objective: nan
Solver model: available
Solver message: Infeasible
Running HiGHS 1.10.0 (git hash: fd86653): Copyright (c) 2025 HiGHS under MIT licence terms
LP linopy-problem-50dnd92w has 81 rows; 33 cols; 129 nonzeros
Coefficient ranges:
Matrix [1e+00, 1e+00]
Cost [2e+01, 2e+01]
Bound [0e+00, 0e+00]
RHS [1e+03, 1e+05]
Presolving model
Problem status detected on presolve: Infeasible
Model name : linopy-problem-50dnd92w
Model status : Infeasible
Objective value : 0.0000000000e+00
HiGHS run time : 0.00
Writing the solution to /tmp/linopy-solve-sffylm6z.sol
('warning', 'infeasible')
The model is unfeasible because the capacity of the link connecting DK1 and DE is not enought to transport 6 GWh in the last time step.
(f) Assume that the pipeline pressure can be increased from 50 to 55 bar, calculate the linepack, i.e., the energy that can be stored in every pipeline by increasing the pressure. Represent this in your pypsa model by adding a store with that capacity at the beginning of every line, calculate the optimal gas flows in every time step and the total system costs.
The energy that can be stored by changing the pressure of the pipeline can be calculated as \(Linepack=\frac{\Delta P}{c^2} A·L·e\) (for this example we assume length \(L\)=1000 km), where we use the energy content (in GJ/tonnes) and convert it to MWh/kg to calculate the linepack in MWh
L = 1000 # km
Delta_P = (55-50)*100000 # Pa
Linepack = (Delta_P/c**2)*A*L*1000*e*0.000277
Linepack
np.float64(9652.383367497767)
network.add("Store", "linepack DE-DK1", bus="bus DE", e_nom=Linepack*600/1000, overwrite=True)
network.add("Store", "linepack DK1-DK2", bus="bus DK1", e_nom=Linepack*200/1000, overwrite=True)
network.add("Store", "linepack DK1-NO", bus="bus DK1", e_nom=Linepack*500/1000, overwrite=True)
network.add("Store", "linepack DK1-SE", bus="bus DK1", e_nom=Linepack*600/1000, overwrite=True)
network.add("Store", "linepack DK2-SE", bus="bus DK2", e_nom=Linepack*100/1000, overwrite=True)
network.stores
| bus | type | carrier | e_nom | e_nom_mod | e_nom_extendable | e_nom_min | e_nom_max | e_min_pu | e_max_pu | ... | sign | marginal_cost | marginal_cost_quadratic | marginal_cost_storage | capital_cost | standing_loss | active | build_year | lifetime | e_nom_opt | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Store | |||||||||||||||||||||
| linepack DE-DK1 | bus DE | 5791.430020 | 0.0 | False | 0.0 | inf | 0.0 | 1.0 | ... | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | True | 0 | inf | 0.0 | ||
| linepack DK1-DK2 | bus DK1 | 1930.476673 | 0.0 | False | 0.0 | inf | 0.0 | 1.0 | ... | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | True | 0 | inf | 0.0 | ||
| linepack DK1-NO | bus DK1 | 4826.191684 | 0.0 | False | 0.0 | inf | 0.0 | 1.0 | ... | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | True | 0 | inf | 0.0 | ||
| linepack DK1-SE | bus DK1 | 5791.430020 | 0.0 | False | 0.0 | inf | 0.0 | 1.0 | ... | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | True | 0 | inf | 0.0 | ||
| linepack DK2-SE | bus DK2 | 965.238337 | 0.0 | False | 0.0 | inf | 0.0 | 1.0 | ... | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | True | 0 | inf | 0.0 |
5 rows × 26 columns
network.optimize()
WARNING:pypsa.consistency:The following buses have carriers which are not defined:
Index(['bus DE', 'bus DK1', 'bus DK2', 'bus NO', 'bus SE'], dtype='object', name='Bus')
WARNING:pypsa.consistency:The following links have carriers which are not defined:
Index(['pipeline DE-DK1', 'pipeline DK1-DK2', 'pipeline DK1-NO',
'pipeline DK1-SE', 'pipeline DK2-SE', 'pipeline DK1-DE',
'pipeline DK2-DK1', 'pipeline NO-DK1', 'pipeline SE-DK1',
'pipeline SE-DK2'],
dtype='object', name='Link')
WARNING:pypsa.consistency:The following stores have carriers which are not defined:
Index(['linepack DE-DK1', 'linepack DK1-DK2', 'linepack DK1-NO',
'linepack DK1-SE', 'linepack DK2-SE'],
dtype='object', name='Store')
INFO:linopy.model: Solve problem using Highs solver
INFO:linopy.io: Writing time: 0.03s
INFO:linopy.constants: Optimization successful:
Status: ok
Termination condition: optimal
Solution: 63 primals, 126 duals
Objective: 3.45e+05
Solver model: available
Solver message: Optimal
INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Link-fix-p-lower, Link-fix-p-upper, Store-fix-e-lower, Store-fix-e-upper, Store-energy_balance were not assigned to the network.
Running HiGHS 1.10.0 (git hash: fd86653): Copyright (c) 2025 HiGHS under MIT licence terms
LP linopy-problem-egx7mas9 has 126 rows; 63 cols; 214 nonzeros
Coefficient ranges:
Matrix [1e+00, 1e+00]
Cost [2e+01, 2e+01]
Bound [0e+00, 0e+00]
RHS [1e+03, 1e+05]
Presolving model
25 rows, 58 cols, 108 nonzeros 0s
15 rows, 48 cols, 88 nonzeros 0s
Dependent equations search running on 15 equations with time limit of 1000.00s
Dependent equations search removed 0 rows and 0 nonzeros in 0.00s (limit = 1000.00s)
15 rows, 42 cols, 78 nonzeros 0s
Presolve : Reductions: rows 15(-111); columns 42(-21); elements 78(-136)
Solving the presolved LP
Using EKK dual simplex solver - serial
Iteration Objective Infeasibilities num(sum)
0 0.0000000000e+00 Pr: 11(17000) 0s
24 3.4466567287e+05 Pr: 0(0) 0s
Solving the original LP from the solution after postsolve
Model name : linopy-problem-egx7mas9
Model status : Optimal
Simplex iterations: 24
Objective value : 3.4466567287e+05
Relative P-D gap : 0.0000000000e+00
HiGHS run time : 0.00
Writing the solution to /tmp/linopy-solve-an4xo_f_.sol
('ok', 'optimal')
network.objective
344665.67287265125
network.links_t
{'efficiency': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'p_set': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'p_min_pu': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'p_max_pu': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'marginal_cost': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'marginal_cost_quadratic': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'stand_by_cost': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'ramp_limit_up': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'ramp_limit_down': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'p0': Link pipeline DE-DK1 pipeline DK1-DK2 pipeline DK1-NO pipeline DK1-SE \
snapshot
0 -0.0 1004.016064 -0.0 -0.0
1 -0.0 2010.044185 -0.0 -0.0
2 -0.0 1004.016064 -0.0 -0.0
Link pipeline DK2-SE pipeline DK1-DE pipeline DK2-DK1 pipeline NO-DK1 \
snapshot
0 -0.000000 3170.637113 -0.0 5226.922401
1 1002.004008 1164.608992 -0.0 5226.922401
2 -0.000000 1737.628389 -0.0 3779.438841
Link pipeline SE-DK1 pipeline SE-DK2
snapshot
0 -0.0 -0.0
1 -0.0 -0.0
2 -0.0 -0.0 ,
'p1': Link pipeline DE-DK1 pipeline DK1-DK2 pipeline DK1-NO pipeline DK1-SE \
snapshot
0 0.0 -1000.000000 0.0 0.0
1 0.0 -2002.004008 0.0 0.0
2 0.0 -1000.000000 0.0 0.0
Link pipeline DK2-SE pipeline DK1-DE pipeline DK2-DK1 pipeline NO-DK1 \
snapshot
0 0.0 -3132.589468 0.0 -5174.653177
1 -1000.0 -1150.633684 0.0 -5174.653177
2 0.0 -1716.776848 0.0 -3741.644453
Link pipeline SE-DK1 pipeline SE-DK2
snapshot
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0 ,
'status': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'mu_lower': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'mu_upper': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'mu_p_set': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'mu_ramp_limit_up': Empty DataFrame
Columns: []
Index: [0, 1, 2],
'mu_ramp_limit_down': Empty DataFrame
Columns: []
Index: [0, 1, 2]}
The model is now feasible because part of the energy to be transmited in the link DE-DK1 can be stored as linepack

